Warrax

Математическое, методологическое, дегенеративное

Давнее из инета (2008 год), решил оформить эту поучительную историю. Очень уж иллюстративно к теме интеллектуального, гм, развития чел-овечества. Причём там даже показывается, как мыслят по-среднестадному. Поучительно.

Авторство и ссылки не простравляю -- обсуждалось много где и я прочёл более 10000 комментов точно, в некоторых обсуждениях их было по несколько тысяч. Порядок цитирования произвольный, в главах объединены цитаты по смыслу, а не по месту написания.

Итак, с чего всё началось -- с поста где-то в инете:

"Есть у меня внучка. Нормальная такая девчонка, смышленая... Пришла вся в слезах. Боится показаться родителям на глаза, поэтому и прибежала к деду. Спрашиваю, что случилось. Говорит, что из-за оценки. Получила тройку и не знает за что.

-- Давай, -- говорю, -- разбираться.

Смотрю... нихера не понимаю".

Казалось бы, от переменны мест слагаемых и множителей результат не изменяется, ergo -- учительница профнепригодна и вообще дура.

Но -- я офигеваю -- появились тысячи комментариев на тему, и многие -- про "так и надо". Давайте разберёмся, кому надо и зачем.

Часть первая, первое обсуждение в инете

В чистой математике, действительно, последовательность указаний именно цифр не важна.
Все верно.
Только мы сейчас не о чистой математике говорим. и мы не фундаментальную математику сейчас обсуждаем.
В 3 или там 5 классе преподают не высшую математику, а преподают именно основу процесса арифметики.
НО !!!! Именно из понимания самой основы потом ученики будут учить, например,физику.
А уж физике, то , уж тут Вы не будете спорить, очень важно понимать, что на ято умножается.
Что расстояние = скорость x время.
или Масса = объем х на плотность.
и т.п.
Именно эту цель и преследует педагогика, когда пытается эту мысль донести.
Именно поэтому учитель и пытается донести до ребенка именно понимание процесса " в натуре" так сказать.
именно на таком простом примере.
Если сейчас ребенок СЕЙЧАС не видит у себя в мозгу этого процесса, как он потом будет учить физику или ,например, химию.

То есть, если умножить плотность на объём, то массы не получится. Ну и если время на скорость -- то будет не расстояние, а что?

Тезис "а потом физику изучать" запомните, далее это будет обсуждаться подробно.

Я не силен в методологии, но у меня сын как раз недавно это проходил. На этом этапе их учат не столько правильно считать, сколько плавно переводят от сложения к умножению.
Умножением считается повторение сложения столько раз, на сколько надо умножить. Т.е. 2*9 - это 2+2+2+2+2+2+2+2+2, а 9*2 - это 9+9.
Понятно, что результат одинаков, но смысл разный. Согласитесь 2+2+2+2+2+2+2+2+2 - это литров, потому что складываются литры.
А 9+9 - это людей (хотя бы потому, что литры тут нигде не фигурируют).

Из комментов: Нихуя. 2*9 – это два, блеать, раза по девять. А не два, девять раз.

Важно: темы для спора -- при наличии мозга -- нет, поскольку речь идёт именно о вычислении, и результат один и тот же. Т.е. как удобнее.

Правильно так;
2 (литра/покупателя) * 9 покупателей = 18 литров. (А не покупателей.)
И меняя местами числа, мы не получаем другого смысла:
9 покупателей * 2 (литра/покупателя) = 18 литров.

(мрачно) Покупатели -- это "штуки", величина безразмерная. Откуда вообще взялись эти литропокупатели, как думаете?

-- Вы отдаёте отчёт в том, что различать 3*4 и 4*3 -- это полный, абсолютный бред? А педагогически опасный ещё и потому, что существуют и в самом деле некоммутирующие величины, некоммутирующие операции -- но это никак, никак не рациональные числа?
-- 3*4=4*3 никто не спорит. А вот если нам надо в 10 корзин положить по 2 яблока и посчитать, сколько всего яблок мы положили, то мы будем делать натурально 2+2+2+... и никак иначе. Мы не можем положить в корзины 10+10 яблок. Только 2+2+2+2+2...

Ещё:

Т.е. полная запись выглядела бы так:
2*9=2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2=18(л), что кстати хорошо отражает реальный процесс,
а
9*2=9 + 9=18, реальный процесс не очень хорошо отражает, да и получается, что 9 покупателей + 9 покупателей = 18 литров.

До слёз (с)

Чтобы понять в чём разница,надо понимать ,что есть умножение.
В арифметике под умножением понимают краткую запись суммы одинаковых слагаемых,где на первом месте число,которое повторяется,а на втором количество повторов.
Если бы это был просто пример,без привязки молоко-покупатели,то главное был бы результат. Для задачи с конкретными образами 9+9 и 2+2+2+2+2+2+2+2+2 это не одно и тоже. Вы согласны?

В арифметике, оказывается, есть литры молока и покупатели.

Все правильно.
Нужно МОЛОКО умножать на ПОКУПАТЕЛЕЙ.
а не наоборот.
это правила формальной логики , вообщето.
если в итоге решения количество МОЛОКА,
то и первым в формуле тоже должно быть именно МОЛОКО.
это же естественно,
что бы получить какое то количество А
нужно соответственно именно А (!!!!!) умножить на В.

Оные литры молока и покупатели -- теперь и в формальной логике.

2*9 и 9*2 - равные, но суть разные вещи. Тот самый разный акцент. Это как сравнивать 3*6 и 2*9 опять равные, но суть разные вещи. А между 2*9 и 9*2 такая же разница как, например, между 6!/10+6 и 54/3 (здесь 6!=1*2*3*4*5*6). Просто в добавок к равенству ещё и похожесть выражений вводит некоторых в заблуждение, что это суть одно и то же.
Вы разве не видите, что числа равные между собой? Что за двойные стандарты? Если для Вас запись 2*9 и 9*2 эквивалентна из-за их равенства, то чем хуже 6!/10+6 или 54/3.
... для математиков 2*9 и 9*2 - разные выражения "по счастливой случайности равные",

Обычно на подобное пишут "где такую траву берёшь?", но я категорически против наркотиков.

зацитирую сюда из обсуждения в другом месте:

Перед учителем стоит задача дать не просто знание сколько, это калькулятор даст, но понимание почему. Это начальная школа, здесь ещё умножают рисунками. Рисуют покупателей, их покупки. В данном случае важно, чтобы ребёнок понял что на что он перемножает. Он перемножает не абстрактные числа, а чашки, молоко, сахар или людей. Решая задачу он представляет покупателей и даёт им молоко, а не a*b. Перемножая в правильной последовательности он демонстрирует и понимание процесса умножения, его "отличие" от сложения, которое тут в основе, и формирует дисциплину ума на основе того, что учительница на уроке вероятно десять раз сказала что на что перемножать и как записать, но не поняв сути ребёнок нарушил заданные условия, и т.д. И это пригодится уже в следующей теме "деление", где перестановка имеет значение и без вот такой вот заданной последовательности ему это будет труднее понять, как и дальнейшую работу со скобками и т.д.. И даже в дальнейшем пригодится, годы спустя, когда вместо того чтоб расписать как получено решение задачи, он будет ставить в конце задачи списанную у соседа цифру и требовать пять, ответ же правильный, и т.д.
Понятие методики вам, похоже, не знакомо и тогда становится не ясно, кто из нас дебил.

Из комментов: Ну бред же сивой кобылы. Если методика, вместо того, чтобы развивать абстрактное мышление, заставляет умножать чашки на молоко, а сахар на людей - нафиг такую методику. Нет никакой "правильной" или "неправильной" последовательности, введение дополнительных необоснованных ограничений пониманию процесса умножения только навредит.

Работа обсуждаемая в данном топике, на мой взгляд, имеет как раз проблему двоякой интерпретации, а не оформления: то ли девочка складывает 9 раз по два литра и делает всё правильно, то ли складывает 2 раза по 9 людей и получает нужные 18, а размерность просто угадывает исходя из вопроса задачи.
Для жюри на конкурсе подобная работа должна была бы стать серьёзной проблемой какое решение принять, но это не конкурс плюс есть возможность спросить у самой ученицы, что она имела в виду. Поэтому поступок учительницы выглядит довольно странно.
Теперь моя позиция Вам понятна?

Из комментов: А почему вы вообще решили, что она что-то складывает? Может она просто перемножает 9 и 2 и получает результат, добросовестно выучив до этого таблицу умножения?

Именно что. При этом зная про коммуникативность умножения действительных чисел, хотя и не такими словами.

Из комментов: дочка в третьем классе.

Дал решить эту задачку. Она решила 9*2 = 18. Спросил, почему.

- Ну, грит, читаем задачу и сразу составляем уравнение 9*2.

- А если бы было условие наоборот, -- спросил я, -- фермер продал по два литра молока 9-ти покупателям, то как бы записала?

- Ну, тогда 2*9, -- ответила дочь.

- А вас учат какой-то правильной записи, там сначала умножаем количество литров на покупателей, а не наоборот?

- Нет, -- ответил ребёнок. -- Нас учат, что от перестановки множителей произведение не меняется.

-- Ну... Как физик, могу вот что сказать: чтобы посчитать пройденный путь, берут скорость и умножают на время. То есть S=v*t. Никто не спорит? Сюда же плотность на объем при вычислении массы, мощность на время для вычисления энергии...
-- А скажите мне как физик, что изменится от того, что я время умножу на скорость? Расстояние изменится?
-- формально ничего не изменится. Просто существуют формулы и их запоминают так, как они выведены. И соответственно цифры подставляют по формуле. Зачем изобретать велосипед, путаться самому и путать окружающих переменой мест в уже веками доказанной формуле?

Запоминте этот твит (с)

Ну и наглядна методология, гм, мышления. Запись формулы перетасовывать обычно смысла нет. Однако такое перетасовывание НЕ является ошибкой! Однако предлагается зазубрить "как положено" БЕЗ понимания сути -- иначе, с пониманием, понятно, что последовательность множителей для натуранльных чисел пофиг.

Ваша внучка, действительно, допустила ошибку, не указав размерность в левой части равенства. Нужно было писать 2л*9 = 18л. А не безразмерные 2*9 = 18 неизвестно откуда взявшихся литров. Равенство неверно, формально можно снижать оценку, насколько сильно - зависит от класса. Другое дело, что от исправления учительницы эта ошибка не исчезает.

Из комментов: Да? Правда?) Скажите тогда пожалуйста, чему же равно тогда 9*2 ?)

Из комментов: Я тут задумался... А какие дать пояснения можно вообще к этой простейшей задаче? В ней же само условие мало отличается от решения. Наверное следует требовать, что ученик составлял к задаче схему. Например, с молоком этим такая схема:

И тут сразу видно, что кто знает таблицу умножения -- тот может и по столбцам складывать и по строкам. Тут и коммутативность сразу видна и есть телодвижения по решению задачи.

Кому-то тут будут видны 3 секции по 6 литров. Опять же для того, кто таблицу умножения помнит, такое решение труда не составляет. Но этот пусть решения можно отбраковывать, как не универсальный: это в данной задаче легко было разбить 3 секции по 6. Было бы покупателей 7 -- не сработало бы.

Для того, кто таблицу умножения плохо помнит, рациональным будет сложить 9+9 -- всего одно сложение.

В общем, задача имеет несколько вариантов решения, и какой из них использовать -- выбирать ученику.

Мнение у меня такое, что при ранней арифметике важна способность именно составить отвлечённую модель задачи и рациональным образом полученную совокупность предметов, пересчитать.

Вот и все, все просто. Нельзя людей умножать на литры. Ответ получим правильный, но логика нарушена. Мы же не просто пример решаем, решаем задачу с условием, есть 9. чел, по 2 литра у каждого, узнаем литры, умножая из на кол. человек--и никак иначе. Учитель не придумывает при оценивании работ ничего, указанную ошибку по методике преподавания математике учитель НЕ ИМЕЕТ ПРАВА не исправить. И этому умножению "литров на людей" учат весь 2 класс... весь 3...продолжают учить в 4... Если девочка до сих пор не усвоила правил решения задач и даже не понимает, что за ошибку исправила учительница, то дело дедушки помочь ребенку понять, что к чему в этих задачах, а не обвинять учителя в злобе и придирчивисти.
Вот так непонимающие и не желающие мирно побеседовать с вполне, зачастую, адекватной учительницей взрослые плодят мифы о непригодности учителей, поселяют в детские головки убеждение, что их вечно гнобят все учителя, а не сами детки в чем-то изволят ошибаться, ну, и прививают отвращение к учебе в целом.
А слабо было дедушке предложить девочке поразмышлять, подумать, в чем здесь могла быть ошибка, логику подключить, вместе с ребенком подискутировать и навести таки ее на правильную мысль, что вряд ли учительница из злобных побуждений перечеркнула решение? (вместо написания возмущенного поста о вполне доброй, надеюсь, учительнице?)))))

Из комментов: То есть снижение оценки на два балла за правильно решенную задачу - это нормально?

Задача решена неправильно, если ход решения записан нелогично. Число в ответе --еще не показатель правильности решения. Например, по физике, умножая не скорость на время, а время на скорость, ученик показывал, что суть решения не понимает, по физике такие перевертыши тоже считали ошибкой, полученныйответ--не само главное еще. Такие требования, с учениками их сотню раз пережевывают, не понять такую чушь--странно. Значит, ни черта не делали на уроке). Вот и все. Тройка законна.

Из комментов: каким образом то, что человек умножает время на скорость, когда "надо" скорость на время, показывает, что не понимает сути решения? %) из чего это следует?

Очень многие дети, выучив наизусть таблицу умножения, (при изучении которой, кстати, и изучается факт про перестановку множителей=произв. не меняется)----ну никак не могут составить действие к конкретной задаче, представляете??))) Ровно пол-класса тормозит на первых порах. Да, вот такая странность (а мало кто из родителей с рождения развивает детей, книжки им читают в день 2 раза вообще единици).
Потому, изучают первые задачи на умножение так---
Сколько у одного!---2 литра. А как узнать, сколько у 9?---2 литра ВЗЯТЬ 9 РАЗ, то еть, 2 х 9. Запишем действие к этой задаче---2 (литра) умножить на 9, получается сколько вего--правильно, 19 литров.
И если ребнок так рассуждать не научится (который задачу с ходу решить не может, а таких у нас пол-класса), то с задачами не двинется дальше. Вот потому и требует учитель четкости и последовательности, вот потому и 2х9, а не наоборот, только в задаче))))
А может, девочка просто наугад действие к задачке написала, так ак изучают сейчас умножение?)))) Взяла 2 числа из текста и перемножила наугад? Учитель это поняла и снизила оценку

Из комментов: Если вы хотите РЕАЛЬНО убедиться что ребенок не просто механически считает, а понимает, почему и как - требуйте словесного обьяснения. .... Самое смешное, что именно такой подход приводит к тому, что дети и не пытаются понять. Напуганные этим бредом, они просто заучивают все "на всякий случай"... на практике рождает то, что мы сейчас видим в коментах - наплыв взрослых людей, которые считают, что НАДО умножать именно в таком порядке. Почему - они не знают, обьяснить внятно не могут, просто НАДО, такое ПРАВИЛО: Так ЛОГИЧНЕЕ. Вот и вырастили "понимание". Люди вообще не знают, что такое математика, что такое логика и так далее. Вот так вот "научили рассуждать".

Логика учителя такова: мы ищем количество ЛИТРОВ, поэтому мы ЛИТРЫ умножаем. Умножая девять ЧЕЛОВЕК на два, мы получили бы 18 ЧЕЛОВЕК.

Из комментов: Что, серьёзно? Если девять человек возьмут каждый по два литра, то получится 18 человек? А вот если по два литра возьмёт каждый из девяти человек, то тогда получится 18 литров?

-- "покупатели - величина безразмерная" - это сильно конечно
-- У вас что, есть возражения? Типа, "школьники встали в два ряда по девять человек. Умножаем пары на ряды: 2 чел. * 9 чел., получаем 18 людей в квадрате". Так, да? Ну, как если метры на метры умножить получим квадратные метры, а здесь получим квадратных людей. Так вы рассуждаете? :)
-- да без проблем. 9 школьников/ряд * 2 ряд = 18 школьников.
-- Ух ты, а откуда взялась размерность "шк./ряд"? Почему 9 - это "шк./ряд", а 2 - это не "шк./шеренгу"?
9 школьников/ряд * 2 школьника/шеренгу = 18 (квадратных школьников/шеренго-ряд). По-моему, очень круто.

Очень мило, да.

Из комментов: Как рассуждают тупорогие ебланы. Они думают так: "в условии сказано 2 ЛИТРА * 9 ПОКУПАТЕЛЕЙ. Значит, нужно перемножить ЛИТРЫ и ПОКУПАТЕЛЕЙ".

И натурально берут и пишут:

2 л * 9 пок

Но тут они внезапно обнаруживают, что в результате получается размерность "л * пок", и это вводит их в ступор. Они-то знают, что должны получиться чистые литры.

"Ааа, ну мы это сейчас исправим", - думают они и делят левую часть на покупателей. И получают в правой литры. Ура, всё сходится.

На самом деле это - подгонка формулы под результат. Грубая ошибка. Показывает непонимание хода вычисления. Почему так происходит? Да потому, что тупорогие ебланы умеют умножать числа, но не размерности. Умножение чисел проходят в школьном курсе арифметики, классе в третьем, а размерности проходят в курсе физики либо в последних классах школы либо в университете. И там учат, когда размерность нужно подставлять, а когда нет.

Так вот: покупатели и банки размерности не имеют. Не потому, что потом сокращаются, а просто не имеют. Соответственно, решение принимает вид:

2л * 9 = 18л

Вот так просто.

Я понимаю, что у вас шаблон: мол, если в условии написано 9 ПОКУПАТЕЛЕЙ, то на 9 ПОКУПАТЕЛЕЙ и нужно умножать. Но надо ведь иногда и голову включать, а?

- Откуда вместо размерности "л" взялась "л/пок"?

- Ну... в похожей задаче мы же взяли и поделили граммы на метры, значит и в этой литры на покупателей поделим.

 

Из комментов: Пример с "человеками" вообще плох. Правильно будет: вчера фермер продал 9 раз по 2 литра молока. сегодня фермер продал 2 раза по 9 литров молока. и вопрос - сколько литров молока продал фермер вчера, и сколько сегодня. И "человек" сокращать не нужно, и коммутативность объясняется.

Тут речь идет не про переместительный закон, а про понимание задачи, что на что умножаем.
Если бы мы решали эту же задачу сложением, была бы разница складывать две девятки или девять двоек.
Посему ввели правило, что первым пишем то, что берем, вторым - сколько раз.

Из комментов: Вот объясните, пожалуйста, чем конкретно вас (или вашего учителя) не устраивает логически формула "9 раз по 2 литра", т.е. 9*2? Почему надо противоестественным образом объяснять, что надо "2 литра умножить на 9 раз" (2*9)? Не кажется ли вам, что второй (ваш) вариант звучит гораздо противоестественнее, чем первый?

Из комментов: Мне кажется, фермеру удобнее спуститься 2 раза в подвал за молоком и принести 2 бидона, чем девять раз спускаться и наполнять покупателям 2-литровые баклажки :-).

Из комментов: Я бы с этим учителем поговорил просто. Изменим задачу на такую: девять участников банкета выпили по две рюмки водки (ну, скажем, за первые десять минут). Сколько всего рюмок водки они выпили? Решение: раз по две рюмки, значит было два тоста. После первого тоста выпито девять рюмок и после второго еще девять. Итого 9+9. Вот пусть теперь мне этот учитель объяснит, почему молоко надо в одном порядке умножать, а водку - в другом."

объясняю, почему вы дура в случае задачки с литрами. двойка имеет размерность не литры, а литры на человека.
как ценник в магазине - руб/кг или руб/шт. или м/с или кв.м на жильца.
Поэтому - абсолютно без разницы, что на что умножать. так как и в случае размерностей аксиома коммутативности операции умножения - выполняется:
(л/чел)*чел=чел*(л/чел) = ЛИТРЫ
(руб/кг)*кг=кг*(руб/кг)=РУБЛИ
вы что,реально идиотка? и носите на кассу 200 кг яблок вместо 200 рублей в зависимости от того, что на что вы умножаете? типа 2кг* 100 руб/кг= килограммы- и вы несете на кассу две тонны яблок вместо денег
а если вы умножите в уме 100 руб/кг*2 кг -то принесете на кассу двести рублей

Из комментов: <имя> проснулась поздно. На будильнике было уже 12 часов/будильник. Она оделась, натянула ровно по одному ботинок/нога и вышла на улицу. Мимо нее медленно проехал трамвай/100 человек, пролетели 10 птиц/до линии горизонта, а также логика/человек и здравый смысл/голова. Но она все еще продолжала возмущаться после вчерашнего - "да как они только смеют думать, что 2*9 и 9*2 это разные вещи. Ведь, мы люди/единицы измерения, точно знаем, что разницы нет! В печь их, по одному человеку/печь" :)

-- Условие задачи: найти произведение 1 кг и 9 км.
Правильный ответ: 9 кг*км.

Пожалуй, я это комментить не буду. Интересно, что это за величина? Что-то Лаэртский вспомнился, песня про фашиста, который от отважного партизана Коли побежал, говно роняя... Но проблема в том, что тогда размерность будет не кг, а кг/км, а вот "умножить килограммы на километры" -- это сильно, да.

В решении этой задачки вполне возможны два вопроса:
Вопрос 1: сколько покупатели унесли молока? Ответ: 9 Х 2 = 18
Вопрос 2: сколько молока было куплено всего? Ответ: 2 Х 9 = 18
Чувствуете разницу?
Есть элементарная логика, которую и нужно соблюдать...
И на которую, похоже выпускники нынешних вузов мало способны...
И никакая математика здесь не при чем.... хе-хе..

0_о

Не, конечно, могли купить и оставить или вылить -- в общем, не уносить -- но это тогда уже явно не про арифметику.

Белинская А. В, Обучение решению задач в начальной школе. Книга для учителя. - М.: Русское слово, 2003 (ГУП ИПК Ульян. Дом печати). - 286 с.

Если некий дебилизм напечатать в книжке, дебилизмом он быть не перестаёт. С чего бы "в ответе будут чашки"?!

Далее будет разобрано подробнее.

Из комментов: Дело не в методике. А в непонимании автором такого понятия как "размерность". Что автор и демонстрирует, утверждая, что если поменять местами множители, сахар превратится в чашки.

Из комментов: А если в каждую из пяти чашек положить сначала по одному куску сахара, а затем по второму:

а) как изменится запись выражения?

б) как изменится размерность результата?

 

Из комментов: Я рассуждал так: за один раз возмём 5 кусков сахара и положим по одному в чашку. За второй - еще 5 кусков и опять положим в чашку по одному. Получается 5 кусков * 2 раза = 10 кусков.

Во все 5 чашек я положил по 2 куска сахара. Всего я положил 10 кусков сахара.

Где я рассуждаю не так?

За что мне снизили оценку?

 

Из комментов: Должен сказать, что автор сего захватывающего математического открытия сам ещё не до конца понял, как далеко оно простирается. Ведь если гипотеза автора верна, то в ответе на месте указанной размерности (которую автор почему-то называет «наименованием») должны быть не «чашки» и «куски», а «чашки*куски». Что, разумеется, совсем не то же самое, что «куски*чашки». Это ж ежу понятно: тут же слова поменяны местами! Но в целом направление мыслей мне очень нравится.

Считаю, надо доразвить. В частности, у первой формулы из примера правильно указанная размерность — «куски + куски + куски + куски + куски». Что резко контрастирует с неправильным вариантом «в чашке + в чашке». Отсюда, кстати, сразу видно, что заменять сложение на умножение тут вообще нельзя — размерность ведь поменяется.

В общем, очень правильное и нанотехнологичное направление мыслей. Но нельзя останавливаться на полдороги. Ведь сколько ещё нам открытий чудных готовит просвещенья дух.

 

Из комментов: А что было бы, если бы чашек было две?

2*2 ≠ 2*2

Шах и мат, мотематека!!1

 

Из комментов: Так... граждане люди дорогие! Я вам как физик и как преподаватель физики говорю: размерность произведения НЕ ЗАВИСИТ от порядка следования сомножителей. Если койки умножить на дни - получатся койко-дни; и если дни умножить на койки - тоже получатся койко-дни. Если литры умножить на безразмерные разы - получатся литры, и если разы умножить на литры - тоже получатся литры!!

Очнитесь, пожалуйста.. Ну вы в магазине каждый день умножаете то количество товара - на цену, то цену на количество товара - и все время получаете РУБЛИ - всегда!

Поэтому. Вводить понятие умножения учитель математики в младшей школе может как угодно - это не мое дело. Я физик, и в не свои дела не лезу. НО!

Утверждать, что при перемене мест сомножителей изменяется размерность итогового результата - то есть произведения - учитель (и методист) младшей школы НЕ ИМЕЕТ НИКАКОГО ПРАВА!!

Потому что размерности и физический смысл задач - это УЖЕ мое дело. Мое, понимаете? Так вот, ответственно вам заявляю - тот, кто говорит, что от перестановки сомножителей меняется размерность результата - ЛЖЕТ. Врет. Нарушает математические и физические законы. Учит детей вредному и неправильному пониманию математических операций и физических законов реального мира. Как угодно это называйте !

Можете меня забанить, но я все-таки скажу. С точки зрения учителя физики подобные умствования про размерности - по типу чашек на куски и кусков на чашки - это признак профнепригодности.

Точка. Можете философствовать как угодно, но от перемены мест сомножителей размерность результата не меняется. Нигде. Никогда.

 

ВОТ ИМЕННО!!! Пока я тут конспектирую комменты из самого первого обсуждения, потом будет чуть подробнее.

 

Из комментов: Мадам, вы лично в магазин когда ходите - и берете 3 кг яблок по цене 100 руб за кг - что делаете? строго следите за собой, чтобы четко умножить 100 на три? и никак не наоборот? Потому что боитесь поволочь на кассу вместо трехсот рублей триста кг яблок - если умножите 3 на 100?

Когда вы просите своего мужа купить хлеба, вы ему что говорите? купи буханки две? или все таки - купи ДВЕ буханки?

 

Из комментов: Нет там никаких человеколитров.

Там количество проданных групп литров умножается на объем каждой группы. В итоге получаем просто литры.

А вот количество этих групп совпадает с количеством людей. Так что никто людей на литры не умножает.

С какой стороны писать количество - абсолютно всё равно. Это дебильные правила, придуманные неграмотным методистом

То число, о котором спрашивается сколько оно учинит, ежели несколько раз взято будет, называется множимое; а то, которое показывает сколько раз оное число взять надлежит, называется множитель. Чего ради и говорится, что оно число надлежит через сие умножать. Напоследок то число, которое через умножение находится, называется произведение.
Ежели кто сложение в умножение переменить хочет, то надобно тогда, как прежде помянуто, искать суммы двух или многих чисел, между собою равных. Чего ради надлежит притом СПЕРВА то число примечать, которому всякому из тех чисел, которые надобно складывать, равно. Оное число употребительным при умножении словом называется число множимое. ПОТОМ надобно примечать, сколько раз оное число должно взять, или много ли есть оных чисел, которые складывать надобно, и которыя все сему числу равны. То число, которое сия изъявляет, называется множитель, а сумма происходящая от сложения тех чисел, которыя множитель изъявляет, и которыя все множимому числу равны, называется произведение или продукт.
// Эйлер Руководство к арифметике для употребления гимназии при имп. Академиии Наук. СПб., 1740.

Из комментов: Вы ошибочно полагаете, что те, кто считает решение задачи верным, отрицают существование множителя и множимого или, вообще, определение умножения через сложение. Вовсе нет. Речь идёт лишь о том, что при решении данной конкретной задачи не имеет принципиального значения порядок сомножителей.

Более того. Ни один из вариантов записи сомножителей в конкретном случае не отражает уровень понимания условия задачи. Степень понимания смысла определяется исходя из выбранного действия (умножение) и того, что именно получили в результате (литры).

 

Из комментов: Множимое - это просто по определению часть операции, стоящая слева от знака умножения, а множитель - справа. Это только и исключительно формальные названия двух операндов для их различения.

Но, уверяю вас, нигде в математике вы не найдете правила, по которому молоко в данной задаче надо назначить множимым, а людей - множителем. Именно в том и заключается основополагающий принцип коммутативности, что вы сами можете их назначить так, как ваша левая нога захочет. А потом в любой момент, и неоднократно, поменять местами, если вам почему-либо первоначальный порядок не нравится.

 

Из комментов: Эйлер. Руководство к арифметике для употребления гимназии при имп. Академиии Наук. СПб., 1740. стр.79.

Обратите внимание на избирательность цитатируемого из Эйлера. Про множимое и множитель -- с пафосом процитировали, а про возможность их перестановки -- аккуратно умолчали. Практически гарантирую, что все, кто за учительницу, целиком текст Эйлера не читали и просто хором перепостили цитату, которую кто-то нарыл и не стал читать далее (либо специально умолчал). Показательно, не так ли?

Только утверждённые методики - иначе получим такое ... методика - это закон.

Из комментов: Итак, суть дискуссии в которую вы влезли со своей руганью:

Одни говорят: "ЛЮБОЙ сомножитель можно взять в качестве множимого."

Другие говорят: - нет только первый.

- Почему нельзя взять второй?

- Потому что так написал методист в нашей методичке. Поэтому на первом этапе будем ставить двойки за 9*2 = 2*9, а на втором этапе – за 9*2 ≠ 2*9... (барабанная дробь) потому что так детям проще.

Занавес.

"методика - это закон" Вы это как юрист говорите, или как поэт? Если как поэт, то простительно. :)))

Здесь люди обсуждают разумность, а не законность, той или иной методики. Похоже, вы даже не понимаете, насколько вы смешны, влезая в это обсуждение со своим "методика - это закон".

ВЫ бредите.
При делении сначала делимое, потом делитель.
При умножении - сначала множимое, потом множитель.
Все предельно логично. И такому положению вещей - сотни лет. А в том, что вы упертый невежа - никто (из нас) не виноват. Разговор о коммутативности.... здесь просто не в тему. Никто ее не оспаривает. Тут вопрос понимания текста (условия задачи) и отражения понимания в условной форме записи, а не решения арифметического примера.
... Вы даже не видите разницы между примерами и задачами, в которых-таки "литры" есть. И при этом смеете оскорблять поучаствовавших в дискуссии (разумеется, на стороне училки) д. ф.-м. н. и к. ф.-м. н. Кроме того вас не смущает, что ваши измышления и выводы противоречат классической математической литературе.
...Ясно одно, менять конвенции - не второклассниково дело, и не дело родственников второклассников, и даже не ваше :), несмотря на всю вашу самонадейность.

Из комментов: Ой, неужели ваше? :) ... Ваши причитания про столетние традиции уже достали… увы, но в качестве критерия истины они не катят. Я уже не говорю о том, что таких традиций нет, напротив, мы пишем 2кг, а не кг2, 2x+3y, а не x2+y3.

...у вас есть только один способ доказать свою правоту, а именно показать на конкретных примерах работу ваших правил и как отразится на результатах вычисления несоблюдение этих правил.

ЛЮБОЙ сомножитель можно взять в качестве множимого или множителя именно в силу коммутативности операции умножения. Но вы этого не поймете никогда.

Ваши домыслы о том, что школьник может не понимать, что он вычисляет количество литров, а не количество покупателей - бред сивой кобылы, т.е. ваш, и школьник в этом не виноват. Если же вы все-таки сомневаетесь, то можете спросить школьника, что он брал и сколько раз. И если вы услышите ответ, что он взял 2 раза по 9 покупателей и получил 18 литров, тогда можете снижать оценку.

Киселёв, «Систематический курс арифметики для средних учебных заведений» (1884)

Это было приведено в качестве иллюстрации "только так, и никак иначе". Но в задаче-то требуется определить количество литров молока, а не умножить 7 на 4 или там 2 на 8. И вычислено правильно -- 18.

И в упор не видят, что на этой же странице написано про сомножители.

Но самое интересное, продолжал я, Не просто складывать и умножать, а знать некоторые удивительные секреты про сложение и умножение. И вот один из таких секретов я вам сейчас покажу. После этого мы рассмотрели два примера: 5+6+7 и 6+8+2. В каждом из них мы делали сложение тремя различными способами: сначала выбирали два числа и складывали их, затем к сумме прибавляли третье число. [Надо было начать с коммутативности.] Каждый раз получалось одно и то же. Я спросил у ребят, почему так получается, и всегда ли будет одно и то же. Без всякого удивления они ответили, что всё это потому, что мы складываем одни и те же числа, и что так будет всегда. Я назвал три очень больших числа, одно из них с миллионами, и спросил, уверены ли они, что для таких больших чисел тоже всё будет правильно. Мальчики согласились, что для таких чисел это может оказаться и неправильным. Тогда как же всё-таки объяснить совпадение результатов у нас? Петя снова повторил тот же аргумент: мы складываем одни и те же числа и, значит, делаем одно и то же.
— Как одно и тоже? — возмутился я.
— Смотри, здесь мы сначала получаем 11 и к нему прибавляем 7, а здесь сначала получаем 13, а к нему прибавляем 5!
— Ну и что? — ответил Петя. А мне так хотелось, чтобы они удивились! Тогда я зашёл с другого конца.
— А что, — спросил я, — если мы делаем одни и те же действия в разном порядке, всегда получится одно и тоже?
— Да, — сказал Петя.
— Ну смотри, Петя, — сказал я. — Допустим, что тебе нужно надеть носки, валенки и галоши. Если ты сначала наденешь носки, потом валенки, а потом галоши, то всё будет хорошо.
(Кивок.)
— Ну а если ты наденешь сначала галоши, потом валенки, а потом носки? Раздался громкий хохот, и мальчики стали наперебой сочинять, что ещё можно неправильно надеть.
— Вот видите, — сказал я, — иногда нужно делать не только правильные действия, но ещё и в правильном порядке.
(Звонкин А. К. Малыши и математика. Домашний кружок для дошкольников — М.: МЦНМО, МИОО, 2006. — 240 с.)

А почему это для чисел "с миллионами" это может оказаться и неправильным?! "Педагог" оставил это утверждение как верное!

Про подмену сложения на любую последовательность действий я вообще молчу. Это не просто профнепригодность, это вредительство.

Тут вообще ничего не множится. Тут складывается. Стоит продавец с молоком. Подходит покупатель. На тебе покупатель 2 литра молока. Подходит второй покупатель. На тебе покупатель 2 литра молока (2+2), подходит третий покупатель, на тебе покупатель 2 литра молока (2+2+2) и т.д. до девяти покупателей.
Если мы складываем 9+9 мы что происходит с покупателями и с молоком? Что мы складываем (складывает, а не умножаем!!!) Литры или покупателей? Покупателей. Столько сколько литров.
Но на кой чёрт складывать покупателей, когда в задаче предлагается складывать молоко, чтоб получить в итоге молоко? Это вы знаете коммутативность умножения, поэтому знаете что разницы нет. А он не знает и чтобы складывать 9+9 надо ввести тут же понятие коммутативности и объяснить почему разницы нет. Что берём 9 покупателей, прибавляем к ним ещё 9 покупателей и получаем литры потому, что мы взяли покупателей столько раз, сколько литров дали каждому. Это трындец какое изнасилование детского мозга, если на одном уроке всё это на него вывалить.

Из комментов: Когда мы проходили умножение, нам это правило давали сразу же. Проклятый Совок!

Из комментов: Основная проблема програм современной школы, я считаю, состоит в том, что оная школа пытается научить детей плавать до того, как они начнут плавать.

В данном случае - пытаются дать некое мифическое "понятие об умножении" - не научив умножать.

В реале всё прекрасно даётся примерно следующим образом:

Дети, а сегодня мы изучим новую приблуду - умножение.

Умножение - это кратное сложение. (Даётся небольшой пример).

Это конечно, удивительно, но правила умножения следующие:

Умножение выполняется справа-налево;

ab = ba;

(ab)c = a(bc);

1a = a1 = a

0a = a0 = 0

А теперь мы будем долго тренироваться на примерах и изучать таблицу умножения.

(Да, меня учили по учебнику Колмогорова - и прекрасно выучили, ни чета нонешним полуобразованным).

 

Лично мне больше всего понравилось "ничего не множится. Тут складывается". Вот даже и не знаю, как это прокомментировать. Представляете, как этот логомысл будет вычислять случай, когда по два литра молока будет покупать не 9 человек, а 999 хотя бы?

Кстати, а если по литру? Вот нельзя, получается, считать 999х1=999, а лишь как 1+1=2, 2+1=3, 3+1=... 98+1=99. Милота!

Просто восхитительно толпа умников демонстрирует полное не понимание основ арифметики.
И неспособность осилить страницу текста который должны понимать школьники младших классов.
Поймите
Произведение
2*5 Обозначает сумму 2+2+2+2+2 которая является решением задачи.
А при перестановки множителей получается произведение
5*2 которое обозначает сумму 5+5 и понятно, что эти 5+5 решением задачи не являются.

Из комментов: Но где в арифметике сказано, что нельзя записывать наоборот? Как могут люди, овладевшие арифметикой, говорить что нельзя записывать наоборот? Что из арифметики следует, что при записи сложения не в том порядке получаются другие величины?

Но может быть хотя бы БСЭ в которой аналогичное определение вы доверяете?
УМНОЖЕНИЕ - арифметическое действие. Обозначается точкой "." или знаком "*" (в буквенном исчислении знаки умножения опускаются). Умножение целых положительных чисел (натуральных чисел) есть действие, позволяющее по двум числам а (множимому) и b (множителю) найти третье число ab (произведение), равное сумме b слагаемых, каждое из которых равно а; а и b называются также сомножителями.

Из комментов: ...авторы БСЭ совершенно правильно написали, что не просто «умножение — это сложение первого множителя столько раз, сколько нам говорит второй», а что «для целых положительных чисел можно найти произведение как сумму b слогаемых, каждое из которых равно a».

Что как бы намекает нам: авторы БСЭ знали математику. Поскольку, во-первых, использовали корректный термин «позволяет», а не «так и только так», и, во-вторых, в явном виде указали, что это выполняется сие только для целых положительных чисел (каковыми размерные величины не являются).

Правда, чтобы понять, почему определение следует писать именно так, как в БСЭ, надо знать математику, а не обучаться наноматематике по методичке нанопрофессора.

2*5 Обозначает сумму 2+2+2+2+2 которая является решением задачи.
А при перестановки множителей получается произведение
5*2 которое обозначает сумму 5+5 и понятно, что эти 5+5 решением задачи не являются.

Из комментов: С какого хрена? 2H₂O - это число "два", повторенное H₂O раз - или, всё-таки молекула H₂O, повторенная два раза?

Меня сейчас ребенок уделал по вопросу 1/2+1/2+1=2.
Фабула: для профилактики врачи порекомендовали пить ребенку лекарственный препарат. В таблетках. Причем в количествах: утром - 1.5, а вечером - 2. Сразу стоит заметить, что ребенку не очень-то нравится глотать таблетки.
Сейчас (вечером) обнаружилось, что у нас в наличии есть одновременно 2 половинки одной таблетки, а остальные - целые.
Предлагаю: "Давай возьмем две половинки и одну целую, а в результате получится две.".
Но ребенок крайне уперто не желал поглощать две половинки одной таблетки, при этом весьма эмоционально спорил со мной, что "половинка плюс половинка не равно одной целой", и, в конце концов, заменил обе половинки одной целой.
Я только спустя минуту понял, что глотать таблетки дважды, несколько проще, нежели трижды. Так что, контекст для ребенка имеет значение.

Из комментов: Это нормальная диалектическая логика.

СЦУКО!!!!!!!!!!!!!!!!

Из комментов: Когда ребёнок не отдаёт себе отчёта в том, что он в данном случае считает не таблетки, а действия, я ещё могу понять. Гораздо более странно, когда взрослые не отдают себе отчёта, что счёт действий и счёт таблеток - это не «контекст», а счёт двух совершенно разных вещей.

(Государственный педагогический институт им. Герцена,
И.Н.Кавун, Н.С.Попова, "Методика преподавания арифметики.
Для учителей начальной школы и студентов педтехникумов"
Допущено Наркомпросом РСФСР, 1934 год)

Из комментов: Нельзя в процессе развития "умения переходить от конкретного к абстрактному" учить заведомо неверным вещам. Ну вот нельзя...

В результате имеем говно в головах уже взрослых людей.

Надеюсь, что автор этого пошёл по статье за вредительство.

При чем здесь формальная логика и какое-то введение?
В обучении своя логика и если учитель акцентирует внимание что надо писать так - то и надо писать так.
Если я прохожу способ решения тригонометрических уравнений с помощью универсальной подстановки, то требую решения заданного уравнения именно с помощью этой подстановки и листочки с иным решением меня не трогают - два и в следующий раз слушай учителя

Из комментов:

(NB: В пояснении пропущена запятая)

Из комментов:

Учитель: -- Дети, сколько будет 5+6?

Маша: -- 11.

Учитель: -- Неправильно, Маша. Садись, два. Ответ 5+6 = 10, потому что число 11 мы еще не проходили...

конечно, конечно...
s=vt- формула расчета расстояний по скорости и времени надеюсь знакома, уже приведенная здесь кем-то.
нигде не пишется наоборот s=tv
А вот именно непонимание разности этих двух одинаковых результатов пораждает неучей,

Из комментов: Это весь аргумент? Тогда извините, мне с идиотами не интересно. s=vt - это традиция, так принято, и так пишут, чтобы было понятнее. Потому что когда все пишут одинаково, проще воспринимать формулы. А здесь даже формулы нет - просто перемножить два числа и все.

Из комментов: Ну это только у тех кто учился в советской школе S=vt и никак иначе. Как вдолбила тупая училка в тупую голову ПТУШника. Любой ВУЗовский препод скажет, что главное - чтобы размерности в правой и левой частях совпадали. Чтобы не получилось "божественное в квадрате" после умножения божественной массы на божественное ускорения.

-- Обращаю внимание - в нашей задаче "В" - это не люди, а количество ПОКУПОК!!!
-- "фермер продал 9 покупателям"- :)

Из комментов: А если бы ПОКУПАТЕЛЬНИЦАМ??? А если бы двое купили два раза? :)) В задачке умножается количество покупок на литры молока (или наоборот), но никак на покупателей. В чем ошибка и ТУПОСТЬ учительницы - она подгоняет под стандарт и не понимает русского языка.

Для тех кто в танке пример

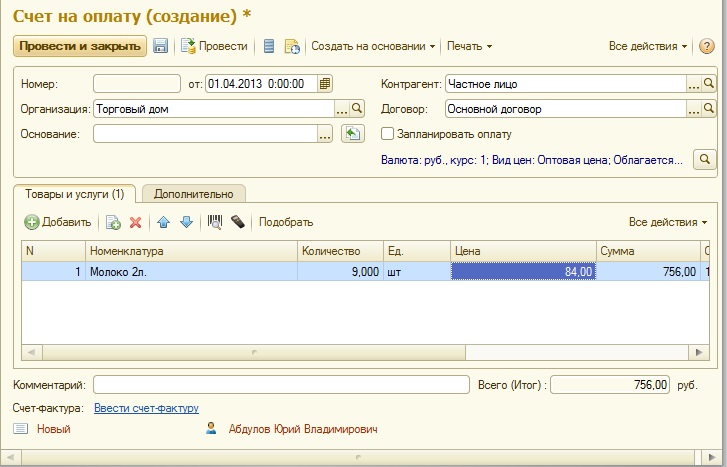
Молоко блеать это товар и с точки зрения товарного учета необходимо умножать товар на проданное количество, училка права

Похоже, всякие истории про бухгалтеров со стороны сисадминов не просто так появились...

Из комментов: Если это, судя по форме, 1с, то порядок столбцов меняется двумя-тремя тремя щелчками мыши. Ну и хуле? ... берем и в программке переставляем столбец "количество" слева от столбца "номенклатура".

Из комментов: Порядок любой. Запутать порядком можно только тупых идиотов и гуманитариев, бухгалтеров недоделанных. Учитель ломает жизнь ребёнку вводя тупые спотолочные правила, а вы его поддерживаете. Вы - гуманитарная гниль, неспособная мыслить. Вы все, кто поддерживает мудака-учителя, которого нужно гнать из профессии. Он множит глупость и вы все этому способствуете.

я уже устал объяснчть, что прирешении арифметических задач, действуют немного другие правила, чем при решении уравнеий.

Из комментов: Немного другие правила арифметики, лол. Немного другое сложение и немного другое умножение? Ну, это разве что для таких, как вы - людей с немного другой анатомией. Вот у вас, например, явно синдром телесной полярности*, так что для вас альтернативная арифметика - в самый раз. Но вас таких пока ещё меньшинство.

* головожопость - прим. ред.

Есть много случаев в математике, когда от перемены мест множителей меняется значение произведения. Поэтому детей учат понимать смысл умножения, а не умножать автоматически.

Из комментов: В данном случае величины скалярны. Поэтому учитель сбивает с толку, отрицая выдуманной методистом формой записи математический закон, по которому умножение работает - не важно 9 раз умножить на 2 литра или наоборот - результат будет одинаков, 18. Это как если бы Вы припарковались на автостоянке в соответствии с разметкой, а подошел бы полицейский и оштрафовал бы за то, что машина стоит капотом к проезжей части, а на нашей стоянке принято наоборот. Вот принято. По закону все правильно, но с вас штраф, два балла.

Второе, допустим, что методист прав. Почему множитель стоит после, а не перед? В чем логика такой записи? Будут уравнения давать, будут переучивать на 9x+2y, когда множитель стоит перед размерной величиной, а не после? Можете обосновать, почему множитель должен стоять после?

не забывайте пжлста, что задача была для начальной школы. И ребенок должен понимать, где тут разы, а где остальное. Чувствовать разницу и все. Про перемены мест слагаемых и множителей - в курсе, мама писала. И главное в задаче, предполагаю, было не найти правильный ответ, а оформить правильно решение задачи.

Из комментов: Ааааааааааааааааааааааааа!!! Вы, случайно, не в страховой компании работаете?

Развели... Множимое Х Множитель = произведение
МНОЖИМОЕ - число, которое помножается на множитель.
МНОЖИТЕЛЬ - действии умножения - число, которое показывает, сколько раз нужно повторить слагаемым множимое, чтобы получить произведение.

Из комментов: Тавышо... а мужики и не знают.

Вы снова, как и многие до вас, приводите ОПРЕДЕЛЕНИЕ что такое уже поставленные в пример множитель и множимое, вкупе с алгоритмом умножения, которые я и без вас знаю.

Но ни вы, ни кто-то иной, так и не смогли привести правила, СОГЛАСНО КОТОРОМУ ЧЕТКО ОПРЕДЕЛЯЕТСЯ, КАКОЕ ЧИСЛО ИЗ УСЛОВИЯ ДОЛЖНО СТАТЬ МНОЖИТЕЛЕМ, А КАКОЕ МНОЖИМЫМ.

И не сможете привести, поскольку это просто неважно. Или, по-вашему, коммутативность придумали идиоты, а вы самая умная? ))

Условие задачи говорит о литрах. Следовательно, результат действия (произведение) следует считать именно в литрах. Неужели это так тяжело понять?

Судя по всему, Вы так и не последовали моему совету, ибо по-прежнему не в состоянии отличить множитель от сомножителя. То, что записи полностью эквиваленты, не имеет отношения к рассматриваемому вопросу. Учитель не зачеркнул равенство 9x2 = 2x9, он отметил, что ученик неправильно понимает смысл операции "умножение" с учетом условия представленной задачи.
Это простительно для ребенка, но для взрослого человека, столь воинственно демонстрирующего собственное невежество, это абсолютно недопустимо!

Из комментов: Это так неудачно выпендриться решили? "Множимое" и "множитель". Опустим на миг, что в нормальной математике для скаляров давно нет никакого multiplicand-а, а есть factor-1 и factor-2. И это именно потому, что как я показал выше, нет правила, по которому множимое должно быть именно количество элементов в группе, а множитель - количество групп, и наоборот.

Это не новая математика. Эта та же математика, по которой всех нас в школе учили. Только это её кулуары. То, чего вы никогда не видели, теперь доступно и шокирует. Это МЕТОДИЧКА. Под "нельзя поменять" подразумевается, что "нельзя менять на данном этапе образовательного процесса". Сначала нельзя менять. А потом будет другая тема, в которой ребёнку объяснят, что если поменять, то результат не изменится. И если включить мозг и озадачиться почему на данном этапе нельзя менять (тут на этом особый акцент, но если уж все такие опупительные педагоги, почему бы не постараться подумать), то можно это сообразить, даже не имея специального педагогического образования. Не всяк сможет, не профессора и не педагоги, но думаю многим это под силу. Но нет, вместо того, чтоб задуматься почему, все хомячки бросились орать какая она идиотка. Неужели вы реально думаете, что профессор математики не знает того, что знает любой не то что взрослый человек, но и школьник средних-старших классов? Боже, как же должно быть раздуто самомнение... и насколько же надо быть жестоким человеком, как относиться к людям, что пытаться унижать человека даже не постаравшись разобраться как и почему... Господи, люди, что же с вами стало... :((
А если ответ будет 3*6, тогда вы согласитесь? Ведь это также тождественно выражениям 2*9 и 9*2. Я думаю к такому выражению тоже можно логику какую-то надуманную приплести.

Из комментов: "от перемены мест множителей произведение не меняется" вы называете "надуманной логикой"?

И так и да: проблема в том, что такие вот методички пишут не математики, а некие педагоги-методисты, которые не понимают математику.

А здесь и нет никакой лирики. Здесь чистая педагогика. Вы понимаете, что это книжка не по математике, а по методике преподавания? Вдумайтесь в словосочетание "методика преподавания". Перед учителем стоит задача дать не просто знание сколько, это калькулятор даст, но понимание почему. Это начальная школа, здесь ещё умножают рисунками. Рисуют покупателей, их покупки. В данном случае важно, чтобы ребёнок понял что на что он перемножает. Он перемножает не абстрактные числа, а чашки, молоко, сахар или людей. Решая задачу он представляет покупателей и даёт им молоко, а не a*b. Перемножая в правильной последовательности он демонстрирует и понимание процесса умножения, его "отличие" от сложения, которое тут в основе, и формирует дисциплину ума на основе того, что учительница на уроке вероятно десять раз сказала что на что перемножать и как записать, но не поняв сути ребёнок нарушил заданные условия, и т.д. И это пригодится уже в следующей теме "деление", где перестановка имеет значение и без вот такой вот заданной последовательности ему это будет труднее понять, как и дальнейшую работу со скобками и т.д.. И даже в дальнейшем пригодится, годы спустя, когда вместо того чтоб расписать как получено решение задачи, он будет ставить в конце задачи списанную у соседа цифру и требовать пять, ответ же правильный, и т.д. Госпидя, да что я распинаюсь. Тут можно полотна текста объяснений написать, но вам ведь всё равно ничего не доказать, верно? :) Потому что вам проще принять, что профессор идиотка, вместо того, чтоб осознать, что может быть вы сами просто чего-то недопонимаете и попытаться это понять. Ещё не увидели связи с самомнением? :)
...как показывает даже вот этот батхед, народу особо и не надо, чтобы их учили. Им важнее справедливость и соответствие обучения их непрофессиональному видению как оно должно быть правильно.

Из комментов: Такой "профессионализм" нам не нужен, нам нужен реальный профессионализм, а не отшибание мотивации у учеников из-за сомнительной методики.

...и переходить от сахара с чашками к абстрактным числам надо как можно быстрее! Ладно, это потом разберём.

Это начальная школа, какие тут к чёрту строго говоря два человека на литр. Они рисунками ещё умножают.
Таблицу умножения же обычно зубрят. Заучивают наизусть без понимания откуда берутся все эти цифры. И не понимают откуда берётся коммутативность. Им просто говорят: да меняйте местами сколько угодно, ничего не изменится. Они и меняют не понимая почему не изменится. В дальнейшем это аукается непониманием и путаницей в других темах. Не видели как книги умножают на парты, получая карандаши в ответе? Или творят чудовищные вещи при делении, где уже нет коммутативности, но из условий задачи не всегда способны понять что на что надо делить. Почему неспособны понять? Да потому что при изучении умножения просто зазубрили и ничерта не поняли как умножение получается из сложения. Неужели всё это действительно так трудно понять, или вам просто хочется, чтобы тётка профессионально занимающаяся педагогикой, была идиоткой, в отличии от вас умного и никакие доводы вас с этого не сдвинут?

Из комментов: Нужно именно это сюда и приплетать. Ребенок, похоже, прекрасно знает о коммутативности и вообще рассуждал, что 9 человек пришли к фермеру и взяли по 2 литра молока. Значит 9 * 2 = 18 литров. Ребенок прав. Ход рассуждений верный. Ответ верный. А то, что он взял группы на первое место, так все равно на следующем уроке говорить о том, что так делать можно.

Из комментов: Хорошо бы тётке, профессионально занимающейся педагогикой, профессионально заниматься и математикой. Потому как высшая математика, в которой числа и арифметические операции над ними выводятся из множеств и отношений, в данном случае более близка всем этим палочкам и кускам, которыми оперирует первоклассник, чем то, что профессиональная тётка выучила в своё время в качестве таблицы умножения 2х9=18. Она может и сильна в методиках, но сам материал, которому она пытается научить, она понимает поверхностно и формально, и потому у неё выходят такие откровения.

Она стремится не к тому, чтобы ученик понял умножение, а к тому, каким строго формальным образом ученик анализировал бы условие задачи и выводил ответ. Почему? А потому что так проще для учителя: пусть ребёнок действует дисциплинированно, как робот, и привыкает к этому с младых ногтей, чем через собственные ошибки дойдёт до понимания. Ведь есть учебный план и нормативные сроки, и детей в классе - не один.

В данном случае тётка как методист свою профессиональную деформацию переносит на детей: они тоже должны уважать Метод. Знание для неё - это знание инструкции, как действовать, чтобы достичь успеха. Почему действовать именно так - это первокласснику знать не положено, и вообще у него ума не хватит. Вместо задания рамок, в пределах которых у ученика есть свобода, задаётся одна единственная колея, по которой надо ученика протащить. Кто по колее идёт без сопротивления - отличник, кто своевольничает - двоечник.

Проще говоря, знание как понимание заменяется практическим навыком БЕЗ понимания.

Любой взрослый увидев эти цифры вспомнит таблицу умножения, где у тотального большинства вызубрено 2*9, а не 9*2. К вопросу о зубрёжке шаблонов.

Из комментов: Чего? О_о Пока что я не встречал людей, которые бы зубрили отдельно 2*9 и 9*2....

Мне коммутативность (хотя слова такого я, конечно, не знал) была чисто визуально очевидна из таблицы умножения. То есть я увидел глазами, что она симметрична (хотя этого слова я, наверно, тоже ещё не знал), потом немонжко подумал и понял, почему оно так будет всегда. Поэтому я асолютно точно никогда не учил 7*8 отдельно от 8*7.

А если ребёнок так отвечает он молодец. И в классе наверняка схлопотал бы пятёрку. Только это не в классе у доски. Это в тетради. Нормальный, умный, понимающий материал ученик сделал бы так, как просила учительница, а при разборе задания в тетради, уже потом, в классе, у доски, выдал бы дополнение, что порядок множителей не важен, и главное объяснил бы почему не важен. Математически, разумеется, а не потому, что папа так сказал. Это была бы пять в тетради и пять у доски. Так надо учиться. А не истерить перед родителями ах мне несправедливые оценки ставят идиоты-учителя.
Поставьте себя на место учительницы. Несколько раз на уроке вы сказали как надо решить эту задачу, и как записать решение. Потом у вас 150 тетрадей на проверку. И вы видите, что сделано не так как вы просили. Что вы поставите? Пять? Скажете: дети, я хочу чтоб первой в решении вы записали эту цифру, а второй эту, так я пойму, что вы поняли материал, потом увидите что сделано не как просили и всё равно поставите пять? Не стоит лицемерить, это неправда. И не один из собравшихся здесь возмущённых хомячков пять бы не поставил.

НЕТ, БЛЯ!!!! Это именно что муштра, а не проверка знаний!

-- Машина ехала 5 часов со скоростью 2 км в час.
Размерность первой величины - часы (время). Размерность второй величины - км/ч.
И неважно, ехала ли машина 5 часов по 2 км/ч, или 2 км в час на протяжении 5 часов, размерность результата с точки зрения физики вообще не изменится и будет км.
так и в той задаче... 2 куска / чашка * 5 чашек, или 5 чашек * 2 куска/чашка....

-- Вы зря умножаете, это же второй класс. Надо СКЛАДЫВАТЬ.
5часов + 5часов это 10 часов
2км + 2км + 2км + 2км + 2км = 10 км
А никаких км/ч на этом этапе НЕТУ.
...
Во втором классе второй множитель - только безразмерный. А нормальное умножение - это третий класс.

Из комментов: В общем я понял, что все не просто плохо, а очень плохо. Под флагом объяснения глупым детям смысла умножения им действительно тихонько подсовывают альтернативную математику, в результате чего она достаточно глубоко укоренилась в массах (масса людей и во взрослом возрасте продолжает считать, что оно так и есть).

Именно так!

Ваша проблема в том, что вас плохо учили в школе. Поэтому вы думаете. что есть какая-то одна, "Истинная математика". А я вот в работе использую минимум три РАЗНЫХ арифметики. В одной из них (a*b)+c = (a+c)(b+c). Это Булева_алгебра и по ней работает вся автоматика. И в лифте, и на крупном заводе. В другой a+1/a=a если a достаточно большое число. и так работает с вещественнными числами ЛЮБОЙ компьютер.

Из комментов: Я знаю, что такое булева алгебра и что такое потеря точности. Но какое это имеет отношение к арифметике натуральных чисел, которую изучают во втором классе. ... И мало того, я совершенно не понимаю, зачем к этой арифметике пристегнули какие то псевдоразмерности.

Более того, в Булевой алгебре вообще нет выражений вида "(a*b)+c = (a+c)(b+c)", да и арифметических сложения и умножения как таковых. Выражения в Булевой алгебре выглядят как-то так:

Конечно, можно вместо специальных обозначений применять знаки умножения и сложения. Типа конъюнкция -- это логическое умножение, а дизъюнкция -- логическое сложение. Но это разве что если надо написать документ на древней пишущей машинке, где, в отличие от компа, нет соответствующих знаков.

Размерности там пристегнуты потому, что абстрактное мышление в 7-8 лет не развито. Практически с натуры:
- Сколько будет 500 плюс 100?
- Не знаю, мы такие числа ещё не проходили
- А 500 рублей и 100 рублей?
- КОНЕЧНО 600 рублей! Вы что думаете, я деньги считать не умею?

...и вот тут надо резко переходить на абстракции!

Разы не множатся на предмет, можно только предмет умножить на разы.

Из комментов: Бли-и-ин, ну что за бред?

25кг - это что, не "разы" разве, умноженные на "килограммы"?

10 кусочков сахара - это что, не разы, умноеженные на предмет?

Вопрос в задачке про проданное молоко. А не про купленное всеми покупателями молоко.
Поэтому строго логически прав ИМХО учитель для которого важен не "правильный" ответ, а логика решения и по-ни-ма-ние ребёнком своих действий. А родитель не понял смысла действий учителя вынес категоричный вердикт.
...Или арифметика понимается как чисто формальная дисциплина утратившая и потерявшая связь с содержанием...
И тогда часы можно складывать с килограммами, а километры с милями
Или она отражает количественные определённости реального качественного мира.
И тогда она не голые цифры, а цифры репрезентирующие.
...Продано то было то же количество молока.
А вот насколько разбавленным водой оказались эти 18 литров, дойдя до покупателя? ab=ba?
Это я просто иллюстрирую что просто 18 литров могут не быть равны 18 литрам. В математической и строго формальной логике между этими 18 литрами никакой разницы нет. Ибо эту разницу не учитывает выбранная методология (родителя), а вот по методологии учителя, который привязывает к содержательной стороне исчислений эта разница может быть в принципе обнаружена.

Из комментов: Какая такая логика применения в нормальной жизни утверждает, что "куплено" != "продано"? Как из этого бреда следует, что трижды два, 2+2+2, можно записать только как 3*2, но не как "взяли два три раза" 2*3? Где связь этого абсурдного требования c "реальной жизнью"?

 

Из комментов: Берем ту же задачу и пусть будет 10 литров и 15693 покупателя, как умножать будете, по методичке (как учитель)?

Из начальной школы, в которой я училась уже так давно, что "люди столько не живут", помню, что в отличие от умножения в абстрактных примерах, где, действительно, от перемены мест сомножителей произведение не меняется, умножение в задачах зависит от содержания задачи, там от перемены мест сомножителей задача утрачивает свой смысл. Умножить число проданных (купленных) литров на число покупателей можно, в итоге мы получаем общее количество литров, а умножить число покупателей на литры нельзя, ибо в итоге получается некорректная величина непонятно кого или чего. Нас учили не только простому умножению, но и логике, умению рассуждать.
Так принято умножать, когда решаешь задачу, а не перемножаешь абстрактные числа. Считается, что размерность зависит от первого сомножителя, т.е., при умножении литров на количество покупателей, в итоге получаются литры, а при обратном умножении количества покупателей на литры в ответе получается величина, которую нельзя обозначить, ведь число покупателей не могло возрасти, а написать в ответе - литров нельзя, так не принято, это противоречит математической логике, используемой при решении задач. Это не "святая уверенность", а просто правило, как и многие другие правила, которым нужно следовать. )
Скорость на время - это физика. А литры на человека - математика, задача для начальной школы. Некоторые моменты, согласно методике обучения, даются упрощённо, т.е. правильное умножение должно быть таким, как объяснил учитель.

Думать не надо! Зубрить надо!

Сомножители и слагаемые равноценны.
Но вы правы - в начальной школе на уроках арифметики с помощью смысловых задач обучают не математическим действиям, а логике применения их в реальной жизни. Для чистой математики существуют т.н. "примеры".
Поэтому училка права, тем более, что действует на основании методик, от которых отступать не имеет права.

Вот тут таки да -- есть обязанность работать по методичке. Но, если методичка такая тупая и ложная, нормальный учитель пояснит, в чём тут дело, а не будет снижать оценку при правильном ответе.

речь шла о математике не как науке, а как об учебном предмете для начальной школы. И учитель учитывает уровень развитости абстрактного мышления ребёнка. Но если этот этап пропустить то вырастет компьютер,которому будет пофиг что считать.

Из комментов: Как степень отказа от умения абстрактно мыслить в пользу зубрёжки вы выдаёте за навык абстрактного мышления?

Этапы обучения -
а. Различение - ребёнка учат различать отдельные понятия, напр. "лево - право", "синий - красный", "тетрадь в клеточку - тетрадь в линеечку"...
б. Запоминание - ребёнок запоминает, как и что, используя, в основном, механическую память.
в. Понимание - ребёнок осмысливает и может объяснить некоторые причинно - следственные связи в изучаемом материале.
г. Применение знаний на практике, действия "по образцу" - НЕОБХОДИМЫЙ этап обучения, т.к., не имея навыков действия "по образцу" и не зная "образцов" человек будет тратить своё время на изобретение давно открытого.
д. Творчество - заключительный этап обучения, человек готов к тому, чтобы самостоятельно добывать и использовать знания. На основе знаний совершенствуются его умения и навыки.
"Зубрёжка", а точнее этап запоминания - необходимый этап обучения, нельзя развивать "креативность" на пустом месте, не имея фундамента.

Из комментов: В данном случае предлагается заучивать неправильное. К чему приводит зубрёжка хуеты, можно видеть на вашем примере.

Я правильно понял, что для вас язык математики, а ведь это тоже язык, -это язык вообще без реальных денотатов?
Такие языки вообще бывают?

Из комментов: Что можно в математике считать денотатами и можно ли, это без меня разбирайтесь, нужно ли разбираться только вот, хз). Речь ведь о чем, в данной задаче учитель нарушает фундаментальное правило, а именно - числа в вычислениях абстрактны и для чисел действительны математические законы, а не представление "как это было на самом деле". Попытки после этого смоделировать "ход мыслей ученика", "ход мыслей учителя" - это ни о чем вообще и к математике не имеет отношения. Повторюсь, присваивать реальные (материальные) смыслы числам в вычислениях - это крайне нелепо и глупо. Чтоб проще, заходите Вы в магазин и видите ценники не в рублях\копейках, а в конкретных наборах купюр и монет, причом строго регламентированных для каждого товара и замена, допустим, 100 руб. на 2 по 50 руб. - запрещена, и как после этого жить?)

Вы смешиваете исходные данные (размерности, названия и пр.), которые относятся к условию задачи (задача ведь может быть любой, по физике, химии, астрономии и пр., и собсно к математике отношения не имеет) и операции с этими данными, чем и занимается математика. Операции (сиречь, вычисления) с математическим объектами (числами) подчиняются математическим законам и эти объекты (числа) в вычислениях - абстрактны. Кстати, для сравнения чисел математика требует, чтоб они были приведены к общему знаменателю, так что пример с 150\15 несколько неудачен;). Как научить ребенка разделять условия задачи и вычисления, абстрагироваться в них, я хз, в идеале привязка к "яблокам, конфетам" должна заканчиваться со счетом на пальцах, но, как Вы правильно заметил, миром правит грубая реальность, поэтому и выходят "специалисты", умеющие что-то одно и сделать практически тоже самое, но в других условиях... эт я технолога искал, блин, 2 месяца убил:)

Вижу, не понимаете. Давайте формализованно на формальной логике
продавец продаёт молоко покупателям: логическая структура суждения, субъекты и предикаты несколько иные, нежели в суждении: покупатели купили молоко у продавца.
Для вас эта разница несущественна, либо в от неё абстрагируетесь,но любой логик объяснит вам.что это разные суждения
Именно эта разница и есть тот зазор между суждениями учителя и недифференцированным восприятием родителя и ребёнка и выражением этой разницы в логике и способе решения задачи.

Не, суждения "продавец продал" и "покупатель купил", конечно, разные. Но какое это имеет отношение к задаче по арифметике для начальных классов?

Разница между проданными и купленными 18 литрами.
"Продано то оно было молоком.
А вот насколько разбавленным водой оказались эти 18 литров, дойдя до покупателя?
Это я просто иллюстрирую что просто 18 литров могут не быть равны 18 литрам. В математической и строго формальной логике между этими 18 литрами никакой разницы нет. Ибо эту разницу не учитывает выбранная методология (родителя), а вот по методологии учителя, который привязывает к содержательной стороне исчислений эта разница может быть в принципе обнаружена
Я пытаюсь вам показать относительность этого числа - 18.
Или подвести вас к пониманию того что 18 литров не всегда равны 18 литрам. ab не равно ba.
Идиотская цель, да?
Например, что 18 литров не равно 18 литрам, если в одних 18 литрах жирность молока 1%, а в других 18 литрах 3.2%

В давней фантастичекской книге Савченко "Открытие себя" был замечательный эпиграф. По памяти: это только в арифметике 2+2=4, в физике уже надо учитывать поправку на дефект массы, а в жизни не то что 2+2, но и 1+1 -- то ли будущая семья, то ли сговор с целью ограбления банка. Но какое всё это имеет отношение к задаче по арифметике для начальных классов?

когнитивно-эволюционный (Ж.Пиаже, Л.Колберг)
На стадии конкретных операций действия с представлениями начинают объединяться, координироваться друг с другом, образуя системы интегрированных действий, называемые операциями. У ребёнка появляются особые познавательные структуры, называемые группировками (например, классификация), благодаря которым ребёнок приобретает способность совершать операции с классами и устанавливать логические отношения между классами, объединяя их в иерархии, тогда как раньше его возможности были ограничены трансдукцией и установлением ассоциативных связей.
Ограниченность этой стадии состоит в том, что операции могут совершаться только с конкретными объектами, но не с высказываниями. Операции логически структурируют совершаемые внешние действия, но аналогичным образом структурировать словесное рассуждение они ещё не могут.
Формальные операции (11—15 лет)
Основная способность, появляющаяся на стадии формальных операций (от 11 приблизительно до 15 лет), — способность иметь дело с возможным, с гипотетическим, а внешнюю действительность воспринимать как частный случай того, что возможно, что могло бы быть. Познание становится гипотетико-дедуктивным. Ребёнок приобретает способность мыслить предложениями и устанавливать формальные отношения (включение, конъюнкция, дизъюнкция и т. п.) между ними. Ребёнок на этой стадии также способен систематически выделить все переменные, существенные для решения задачи, и систематически перебрать все возможные комбинации этих переменных.

А до 11 лет ребёнок не может мыслить предложениями, что ли?

Всё просто: да, интеллектуальное большинство мыслит шаблонами и т.д. и т.п. Но вопроса-то по сути дела два.

Первый -- неадекватность методички с математической точки зрения.

Второй -- недопустимость снижения оценки за правильный ответ.

Интеллектуальное развитие не эквивалентно паспортному возрасту. Может быть как отставание, так и опережение. И категорически недопустимо "обрезать крылья" развитым детям. В данном конкретном случае учительница могла спросить, почему написано именно так -- и убедиться (или же нет) в понимании примера. А она тупо снизила оценку за правильный ответ, полученный другим способом. Профнепригодность!

давайте опишем завтрак - яйца - 2 шт, кофе - 1 шт, печеньки -4 шт. Переставьте местами множители и множимое. Посмотрим что получится.:)

Два яйца, четыре печеньки и одна чашка кофе. И что?

Для младших школьников совершенно неочевидно, что исходная задача про человеков и литров аналогична задаче о количестве элементов в прямоугольнике. Потом, когда понятие абстрактного числа становится привычным, это можно и показать.

Из комментов: А мне кажется, все с точностью наоборот. Все же начинается с таблицы умножения, а это именно абстрактные числа, а не литры и человеки. И что вообще сложного в понятии абстрактного числа? Вы считаете, что для детей 2 яблока - это не то же количество, что 2 груши?

Понятно, что сначала надо определить умножение через сложение. Но сразу после этого надо рассказать про количество элементов в прямоугольнике (что же в этом сложного?) и на это дальше и ориентироваться, включая таблицу умножения. А если где-то учат умножению без объяснения его коммутативности и прохождения таблицы умножения, и вместо этого заставляют каждый раз складывать (2+2+.... или 9+9+....), то, по-моему, учат неправильно.

P.S. Кстати, процитирую по этому поводу Арнольда: "Коммутативность умножения можно понять, только пересчитывая по рядам и шеренгам выстроенную роту солдат или же вычисляя двумя способами площадь прямоугольника. Все попытки избежать этого вмешательства реального мира в математику - сектантство, которое восстанавливает против себя любого разумного человека и вызывает у него отвращение к этой науке, к умножению и к любым доказательствам."

 

Из комментов: Как показывает опыт Бурбаки, при подобной педагогической практике создания формальных алгоритмов решения на любые, в том числе простые, вещи, дети именно пишут циферки без малейшего проблеска осознания своих действий. "Поставь литры первыми, а людей вторыми" - типичный формальный алгоритм. Потому что если ребенок действительно понимает, что делает, то он понимает так же, что 2*9 и 9*2 абсолютно равнозначные пути решения.

А иначе ребенок вырастет и превратится во что-то вроде вас.

 

Из комментов: Натуральные числа не перестают быть полугруппой по сложению, даже если их проходят в школе. Просто надо не заваливать детей бурбаковскими абстракциями, а объяснять им на пальцах на понятном им языке. Как показывает моя практика, дети при этом способны понять такое, что папа с мамой плакали навзрыд.

А по делу - фиговый учитель, не знающий предмет, никогда не будет авторитетом. И ничему он класс не научит, не потому, что он не авторитет, а потому, что он фиговый учитель.

с точки зрения профессиональных математиков, у нас тут N рассматривается как полукольцо опеаторов R+ → R+ , поскольку оператор [практически] всегда пишется до операнда, то единственная осмысленная запись это 9*2.

Из комментов: Кстати, отменный ответ. Если переводить с алгебраического на обычный, то, обозначив за X количество молока, проданное одному покупателю, мы получаем, что в сумме продано было 9X литров. Следовательно, подставив за X двойку, выходит, что продано 9*2 литров. Если бы тут была какая-то некоммутативная операция, то это было бы совершенно правильными действиями.

Например, мы кипятим 2 литра молока в маленькой кастрюльке и получаем 1,5 литр кипяченого молока за счет испарения. А если мы это сделаем в большой кастрюльке на 9 литров, то получим 8,5 литров молока за счет относительно меньшей площади поверхности испарения (цифры взяты с потолка, но суть в том что при любом обьме ровно пол-литра молока испаряется). Жена фермера кипятит это молоко и поит им детей, который у нее 9. Соответственно, она нагревает каждому по кастрюльке: операция a|b= a*(b-0.5) , если дети выпивают 2|9 (два ребенка и 9 литров холодного молока на каждого), то они выпивают 17 литров, а если 9|2, то они выпивают 13,5 литров. При этом операция задана именно как a*(b-0.5), потому что число детей - оператор, а число литров, которое мы рассчитываем - операнд, соответственно математически правильно записать эту операцию именно так, хотя если ты напишешь a|b= (a-0.5)*b , коллеги тебя скорее всего не расстреляют.

А как лично вы считаете, двойка за ответ школьника "квадратное уравнение с отрицательным дискриминантом имеет 2 корня" - это правильно, или неправильно? Вы слишком привязались к некоей абстрактной и непоколебимой Истине. А, как известно, следующий градус посвящения начинается с опровержения постулатов предыдущего.

Из комментов: Правильно, если он сумеет внятно объяснить, что такое мнимая единица, а также как складывать и умножать комплексные числа. Иначе неправильно.

Ровно так же, как с нулевым дискриминантом: два корня правильно, если скажет, что с учетом кратности и воспроизведет (x-3)(x-3)=0. Иначе неправильно.

Замечу, что постулаты предыдущего не так, чтобы опровергаются; скорее, показываются границы их применимости. Нет действительных корней, ага.

Хотя тут скользкий момент. Дифференцирование и интегрирование в школе дается без теории пределов. Если у учителя есть на это право, он должен смириться с тем, что ученик может взять несобственный интеграл, хотя его этому не учили. И также должен понимать, что ученик, знающий про комплексные числа, про которые в иных школах (г. Королев М.О., 11-я, выпуск 1998) не рассказывают, не обязан, задействовав мнимую единицу, доказывать аналитичность голоморфных функций.

 

Из комментов: Книга "Arithmetic & its Applications", D.P.Colburn, 1856. Раздел под названием "Multiplication", стр. 76 и далее. Обратите внимание, что четко разделены multiplicand и multiplier, соответствующие в русской терминологии множимому и множителю. Любопытно, что "нормативный" порядок в этой книге противопожен русскому! По-русски учебники, которые настаивают на нормативном порядке, в записи 2*9 определяют 2 как множимое, 9 как множитель, а смысл действия как 'взять 2 девять раз'. Тут наоборот 2*9 означает "взять 9 два раза", и это вполне логично, потому что словами это говорится "2 times 9", т.е. дословно именно "два раза девять".

На странице 79 мы читаем:

NOTE: In changing the order of factors the one taken for the multiplier should always be regarded as an abstract number (see 74g) the other should take the denomination of the original multiplicand. Thus 4 times 3 apples = 12 apples etc.

Здесь "abstract number" как раз означает безразмерное число, а "denomination" - размерность (литры, человеки итд.). То есть, если следовать этим правилам и применить их к задаче про 18 литров, как раз надо записать 9 * 2 литра = 18 литров, но никак на 2 литра * 9 = 18 литров - это неправильно, потому что первый множитель это всегда число "раз", абстрактное, безразмерное число.

Это принятая условность. У англичан безразмерный множитель принято ставить на первое место, а у нас на второе. И в жизни вообще, и в математике в частности, есть ещё много других условностей. Может, не все их нужно запоминать, всё зависит от того, есть вам от этого какая-то польза или нет.

Может быть, именно эта условность (порядок множителей в задачах для второго класса) вам в жизни никогда больше не пригодится, тогда вам это и запоминать не нужно. Я, например, этого не помнила

Из комментов: Это самое точное замечание. Вот именно - это условность. Жаль, что такая условность способна отбить у 7-8-летнего ребенка НАВСЕГДА тягу к знаниям и стремление к учебе... Мы, взрослые, сейчас обсуждаем кучу научных трактатов и ищем подтверждение своего мнения. И до конца не находим, потому вступаем в дискуссии. А для ребенка эта тройка ВАЖНА - это его личная трагедия, если хотите. И не поймет он низачто, почему он, дав правильный ответ, тройку получил. Вопрос в том, ЧТО эта ТРОЙКА за условность может значить для ребенка. Кто об этом подумал?

Часть вторая, математика по Киселёву

А.П.Киселёв "Систематический курс арифметики":

"Принято обозначать умножение посредством особого знака. Если, например, 7 надо умножить на 4, то пишут так: 7х4, или 7.4, т.е. пишут МНОЖИМОЕ, СПРАВА ОТ НЕГО ЗНАК УМНОЖЕНИЯ (КОСОЙ КРЕСТ ИЛИ ТОЧКА), А СПРАВА ОТ ЗНАКА СТАВЯТ МНОЖИТЕЛЯ"

Из комментов: А где в этих выраженях сказано, что количество покупателей не может быть множимым, а количество молока множителем?

Легко найду в цитируемом учебнике, который тщетно призываю всех прочитать. Слушайте внимательно, с. 37:

"Множитель всегда число отвлеченное, так как он означает, сколько раз множимое должно быть повторено слагаемым; множимое может означать единицы какого-угодно названия, например, аршины, рубли, карандаши и т.п.; произведение означает единицы того же названия, как и множимое; так если семь рублей умножается на 4, то получается 28 рублей". (там приводился пример задачи, когда 4 тетради по семь рублей (копеек), и нужно найти сколько они стоят).

Выше я уже приводила определение из этого учебника, по которому множимое ставится на первом месте, а множитель на втором (см. с. 36).

В "нашей" задаче множимым являются литры ("единицы какого угодно назания"). Они же (литры) получаются в произведении. Множитель же (9) ставим на втором месте. Вот и все.

 

biglebowsky: Вот задачка, причем - на совершенно бытовом уровне.

Работаем с чертежом "вид сверху", на котором изображен план прямоугольной комнаты, стороны комнаты 6м и 3м.

Надо вычислить площадь этой комнаты, результат вычислений отнести в БТИ и ЖЭК. Эти организации принимают данные по площадям, измеренные в м².

Каким образом по Киселеву эту задачку решать будете?

 

Итак, смотрим учебник Киселева:

"Множитель ВСЕГДА число отвлеченное, так как оно означает, сколько раз множимое должно быть повторено слагаемым; множимое может означать единицы какого угодно названия, напр., аршины, рубли…."

Вычисляем площадь комнаты (длина 6 м, ширина 3 м) в строгом соответствии с правилами и определениями данными Киселевым:

6м * 3 = 6м + 6м + 6м = 18 м

Странно, вместо площади у нас получилась длина.

Может быть, надо так:

3м * 6 = 3м + 3м + 3м + 3м + 3м + 3м = 18 м

Теперь получилась ширина. Но нам-то нужна площадь в метрах КВАДРАТНЫХ.

Как быть?

 

И чтоб 2 раза не вставать, как по тем же правилам вычислить напряжение, например, если: ток I = 2 A, сопротивление R = 3 Ом?

Если 2А * 3 = 2А + 2А + 2А = 6А - получаем амперы, а хотелось бы вольты.

Если 3Ом * 2 = 3Ом + 3Ом = 6Ом - опять не то.

Как быть? И как определить где тут группы с разами?

А. П. Киселев — это эпоха в педагогике и преподавании математики в средней школе. Его учебники математики установили рекорд долговечности, оставаясь свыше 60 лет самыми стабильными учебниками в отечественной школе, и на многие десятилетия определили уровень математической подготовки нескольких поколений граждан нашей страны
Потому что все новые учебники ориентированы на Науку, а точнее, на наукообразие и полностью игнорируют Ученика, психологию его восприятия, которую умели учитывать старые учебники. Именно "высокий теоретический уровень" современных учебников — коренная причина катастрофического падения качества обучения и знаний. Причина эта действует более тридцати лет, не позволяя хоть как-то исправить ситуацию.

Тут что важно понимать: преподавание математики, если это действительно математика, должно быть математическим, с как можно более быстрым переходом в абстракцию Это вообще для мышления полезно. Однако требует достаточно высокого интеллекта, который у ребёнка должны развивать ещё до школы в семье.

Но интеллектуальное большинство на подобное не способно (и родители тоже), и эта самая педагогика направляется на попытки научить хоть чему-то того, кто нормально мыслить не способен и вообще не желает. И это не признак маргинальшины -- в т.н. высшем свете подобное называли салонным слабоумием. Т.е. человек может рассчитаться в магазине и даже поделить о,5 на три без остатка -- по семь бульков каждому. Аналогия для грамотности: читать может, но проговаривая про себя слова и медленно, усваивать смысл длинных текстов не может.

Вот для таких и предназначена "ориентация на ученика", которая оказывается несовместимой с "ориентацией на науку", что показательно. Аналогия: обучение чтению по слогам и вслух, когда надо читать подряд и без проговаривания слов. Да, не все так могут в первом классе; но педагогика учит троечников и забивает на развитых детей. До сих пор помню, как в первом классе с меня требовали чтение по слогам, когда я уже спокойно читал толстые книжки без картинок, а по слогам никогда и не пробовал, так как незачем. Не сложно, но на хрена?!

еще один убийственный аргумент, — "у Киселева есть ошибки" (проф. Н. X. Розов). Интересно, какие же? Оказывается, — пропуски логических шагов в доказательствах.
Но это же не ошибки, это сознательные, педагогически оправданные пропуски, облегчающие понимание. Это — классический методический принцип русской педагогики: "не следует стремиться сразу к строго логическому обоснованию того или иного математического факта. Для школы вполне приемлемы "логические скачки через интуицию", обеспечивающие необходимую доступность учебного материала"

Очень странное понимание понимания, я бы сказал. Не, кое-что приходится упрощать, да. Но логические пробелы -- это не понимание, а зубрёжка.

biglebowsky: Замечательно! Но объясните, почему школьники при решении задач по физики должны следовать этим амбарным правилам?! И вам здесь приводили примеры таких задач, где пресловутое правило определения "размерности", пардон, "названия единицы произведения" из арифметики Киселева просто парализует вычисление. (Собственно, это единственный пункт, вокруг которого разгорелся сыр-бор. )

Дело в том, что решение любой задачи, связанной с математическими вычислениями, можно разделить на два этапа:

1 – моделирование,

2 – вычисление.

Задача моделирования - построить математическое выражение, т.е. проще говоря, перевести условие задачи с русского языка на математический. При этом, если задача из физики, берутся соответствующие физические формулы и из них или на основании их строится математическое выражение. А теперь внимание: именно эти ФИЗИЧЕСКИЕ формулы определяют, где и какие единицы измерения будут использоваться и какая размерность будет у результата вычисления, а не амбарные правила Киселева.

Далее построенное математическое выражение попадает в руки математика, который делает соответствующие вычисления, при этом он не обращает никакого внимания на единицы измерения, он работает не с литрами, метрами и секундами, а с теми самыми множими и множителями, делимыми и делителями, степенями и основаниями и т.д. И ему совершенно не интересно почему у вас 2*9 а не 9*2 (кстати, если считать на деревянных счетах, то удобней все-таки 9*2, т.е. 2 раза по девять :)

Что касается магазинных чеков, то это вообще не арифметика – это бухучет называется.

От себя дополню: чтобы "по Киселеву" определить площадь, нужно взять его учебник геометрии.
А если вам хочется представить вычисление площади именно как суммирование (умножение), то чтобы в произведении получились квадратные метры, надо, чтобы они же были в множимом.
Итак: имеется ряд, в котором выстроены один за другим шесть квадратных метров (квардатики такие :)).
Всего рядов 3.
6 квадратных метров х 3 = 18 квадратых метров.
НАШИ математические традиции незыблимы. Справьтесь у своих свиней, они в теме.

biglebowsky: -- Восхитительно!...

Радиус круга 2м. Требуется вычислить площадь круга. Где тут квадратики рядами?

 

Из комментов: вы - позорите мою альма-матер. и ФМШ заодно.

Умножение не определяется через сложение, а вводится для маленьких детей - на примере натурального счета. Всю жизнь в школе новый материал сначала вводится на некоторых примерах и рассуждениях, а потом все это доказывается. Это раз.

И два - 5*3 - это еще и 5 раз по 3, 3+3+3+3+3 - и как вводить умножение - на какое место ставить "множимое" - абсолютно - слышите вы - АБСОЛЮТНО однофигственно.

Обычно это делают так, как удобнее для носителя языка - если в языке числительные обычно употребляются ПЕРЕД объектами - как например, в английском языке - то умножение детям вводится именно как

a*b=b+b+b.. a раз. Загляните в англоязычные методички для младших школьников - убедитесь, блин сами!

Почему в русском языке появилась эта хрень про "буханки хлеба 3"- я не очень точно помню, но, кажется, связано с вопросами адаптации иностранцев-преподавателей арифметики при Петре I. Кажется, голландцы нам подсуропили - но точно не знаю, врать не буду.

Так вот, еще в 40-х годах академик Арнольд - вы, я надеюсь, помните из своего фмшашного и мгушного прошлого, кто это - писал о том, что этот случайный языковой фактор, усложняющий преподавание арифметики в школе - должен быть устранен, и то, что считается множителем - должно быть поставлено НА ПЕРВОЕ МЕСТО!

И так в общем и было довольно долгое время. По крайней мере я в личном своем опыте никогда не сталкивалась с дебилизмом - заставьте детей корячиться с "литров взять два раза ", бо это имеет какой то сакральный смысел.

Смысела нет, а результатом этой дряни является то, что даже граждане из ФМШ и МГУ нихера не знают обычной школьной арифметики.

Часть третья, о том, к чему приводит

Из комментов:

-- нашел книгу этого автора, но не ту, что в заголовке, так там еще круче. Итак "Белошистая А.В. Методика обучения математике в начальной школе", страница 351:

"при решении 3адачи вторым способом можно ввести термин <скорость сближения>, разъяснив его по графической модели.

Учитель может сдвигать одновременно навстречу друг другу фигурки пешеходов, каждый раз на одно деление. Это значит, что прошел 1 нас пути.

На сколько приблизились (сблизились) друг к другу за 1 час пешеходы? (на 5 + 6 = 11 км/ч)

Обращаем внимание детей на то, что складываются скорости, поэтому в наименовании ответа тоже скорость".

держите меня!!!!! пешеходы сблизились на 11 км\час (!!!)

Без комментариев.

-- я вспомнил, что нам во втором классе (72 г., районная московская школа) говорили таки "вообще-то есть такое правило, что надо писать сперва что умножаем, а потом сколько раз берем, но мы-то с вами знаем, что от перемены мест сомножителей произведение не меняется, так что пишите как хотите." Хорошая была училка, стало быть.

-- В этом споре об умножении ярко проявилась очень интересная особенность мышления многих людей: они готовы, не опровергая с детства усвоенной аксиоматики, допускать параллельное существование совершенно противоположных утверждений, верных именно для данного случая. Ведь все знают, что от перестановки мест и т.д. Но! Вот здесь правильно будет по-другому, потому что … и дальше "новая логика".

Если усложнить условие и объяснить собеседнику, что такие задачи можно подавать с разной логикой: со стороны "человека" (девять человек взяли по две бутылки) и со стороны "бутылок" (бутылки порциями по две были разобраны девятью покупателями), собеседник начинает сопротивляться и выдумывать совсем уже занимательные построения. Потому что "вещи" и "разы", оказывается, легко меняются местами, а переместительный закон покоится на неком мощном фундаменте. И это еще не доходя до анализа размерности, там вообще логический швах начинается.

То есть "не укради" без сомнения и легко уживается с готовностью унести с работы все что угодно, при этом сам несун искренне не понимает, почему его называют вором. И очень сильно сопротивляется, когда все-таки приходится признать явное надувательство во всех его "логических" построениях. Безусловно, и привлечение авторитетов присутствует, как же без него - то ли методички, то ли экспроприация экспрорпиаторов.

Верно: такие вот "параллельные логики", если уж образуются, действуют по жизни в целом. "А нас-то за шо?!" -- типисный пример.

-- Понимаете, любая метода, какой бы она ни была прекрасной в теории и на страницах методички, познается и проверятся практикой. А, как показывают комментарии ко всему этому срачу, эту проверку она тупо проваливает. Потому что мы имеем взрослых уже людей, которые бьет себя пяткой в грудь, крича что "так логичнее", "меня так учили " и " есть такое правило - размерность результата зависит от размерности первого множителя". Такого правила НЕТ; более того, оно противоречит физике.

Что приводит нас к тому, что в коментах мы имеем также учителей физики, которые МАТЕРЯТ эту методу и мечтают повесить "училку на суку", потому что им потом приходится переучивать людей, которые зарубили себе мантру "литры на покупателей - литры, покупатели на литры - литры". Причем, как оказывается, это серьезная проблема. Вот и все. Все очень просто на самом деле. С высоты наших " абстракций", а на самом деле опыта и знания реалий настоящей науки, мы видим что эта методика - очень вредна, искажает суть, приводит к недразумениям, которые потом уже не выколотить из взрослых людей и прочее.

-- Вчера у меня случился когнитивный диссонанс на этой почве. Как раз вчера дочке задали такие примеры на умножение. Посмотрел, увидел, что всё у неё сделано "неправильно", потом посмотрел на образец в учебнике, увидел, что там тоже все примеры написаны наоборот, хотел уже объяснить, как надо, но потом подумал, что, может, из-за иврита их так учат.

-- У меня в школе было круче. Классе во втором или третьем было 2-21=?

Я сказал -19, а учительница настаивала что ответ 0, "потому что отрицательные числа мы ещё не проходили" и "если ты знаешь, то молчи, только одноклассников путаешь" и тоже оценку снизила, потому что я настаивал на своём. 96-97 годы, до сих пор помню.

Показательно, не так ли?

-- «А моего ребенка учили ровно наоборот: если пять чашек ПО два куска, то надо умножать пять на два. Умножается на то, ПО сколько. Во всяком случае, мне дитя так объясняло. Вот буквально только что учили, все первое полугодие. А во втором появилась задача: "В одной деревне 7 улиц по 5 домов, в другой 5 улиц по 8 домов. В какой деревне больше домов? Можно ли ответить на этот вопрос, не производя умножение?" И двадцать пять человек сказали - нельзя. И пятьдесят родителей плюс учительница мучительно пытались выкрутиться из этой ситуации и объяснить детям, не разрушая авторитета учебника, что таки можно.

Наглядненько.

-- Выше было верно сказано кто не может учить - тот учит как учить. Я преподаватель техникума и с подготовкой своих студентов по школьной программе знаком очень хорошо. Этот учитель учит ребенка действовать только по одному алгоритму, соответственно, дети и привыкают действовать только по алгоритму, а в итоге стоит немного изменить условия задач (уйти от алгоритма) - сразу начинаются проблемы. Не могут сейчас дети после школы решать задачи, если они не соответствуют примеру, который дает учитель. У многих совсем забито мышление и они ни в какую не готовы выйти за рамки, чтобы получить что-то новое.

Роботы-исполнители.

-- Я уже четвертый месяц бьюсь над тем, чтобы у ребенка до автоматизма дошло понимание, что 3+7 и 7+3 - это ОДНО И ТО ЖЕ. Я долго не могла понять, КАК можно НАСТОЛЬКО исковеркать детское сознание!!! Дети же вам верят, больше чем родителям!!!! ПИДАХОГИ (дальше у меня только матом, извините, откланяюсь)

Исправлять всё куда сложнее, чем обучить чему-то простому с нуля.

-- Господа педагоги, собравшиеся здесь! Защитники методологии!

Я пока что еще способен понять отличие математики от педагогики, поэтому и обращаюсь к вам.

Вы делаете страшную и опасную вещь. Вы отказываете ребенку в праве догадаться о чем-то самому. Вы отказываете ребенку в праве на самостоятельность мышления. И главное - вы обманываете ребенка, утверждая, что эту задачу должно решать единственным способом. Во втором классе вы говорите, что надо делать так, а вот так делать нельзя. А через год скажете, что "вот так" на самом деле можно. Какие выводы из этого сделает ребенок еще через год?

Уважаемые педагоги, открою вам страшную тайну: дети, на самом деле, очень хорошо чувствуют, когда их обманывают. И когда-нибудь отомстят вам за это.

И еще одну страшную тайну открою: у детей (с возрастом это проходит) еще очень развиты воображение и любопытство - качества, которые вы, как педагоги, должны бы всячески использовать и культивировать. Но вы делаете наоборот - изничтожаете и вытаптываете их. Потому что так проще. Вот вы придумали какой-то способ объяснить ребенку, как складывать и умножать. Но вы, наверно, очень удивитесь, узнав, сколько еще способов решения задачи о молоке способен придумать ребенок самостоятельно, если дать ему вводные, основополагающие (показать на палочках), и - заинтересовать. Но это слишком сложно, да. Самое трудное - заинтересовать. Это действительно очень непростой и спорный вопрос педагогики, так что не буду углубляться...

Вот, например, исходную задачу о девяти человеках с двумя литрами молока на каждого ребенок может решить не только как 2*9 или 9*2, но и (вы не поверите!) через формулу 6*3! Как? Объясняю. Ну вот сложно мне, ребенку, представить у себя в голове одновременно девять человек, и у каждого по бидону с молоком. Я могу представить только трех. И я уже умею, предположим, делить на три. Я поделю группу в девять человек на три группы по три человека. И мне уже нетрудно представить в воображении группу из трех человек с бидонами по два литра, и я уже могу посчитать, что литров в этой группе будет шесть. Остается только умножить шесть на три и, вуаля - искомый результат! Так вот, господа, это и есть математика!

Вы же, вместо того, чтоб поощрить математические способности этого ребенка, поставите ему двойку и заставите решать задачу так, как удобно учителю - так, как написано в методичке.

...и сказанное относится не только к математике, что важно понимать. Множество людей (большинство!) ментально кастрируют в детстве, когда вместо ответоа на вопросы отвечают "так положено", "все так делают", "мал ещё знать", "старших надо слушать и слушаться, что бы они не говорили" и проч..

--Не могу удержаться от комментария.

Я тоже учился в школе... в СССР. 9-й и 10-й классы в школе АПН СССР в классе с суперуглубленным изучением математики. Наверное, знаний по математике у меня больше чем у любого учителя типа упомянутой Белошистой. Я и сейчас люблю математику и иногда решаю какие-нибудь задачи, хотя от науки в данное время далек.

Тот учитель, который поддерживает Белошистую и считает, что оценка поставлена верно - идиот, которого от математики надо гнать метлой. Математика, несмотря на строгость цифр, наука творческая. Одну и ту же задачу можно решать разными способами. На экзамене в МГУ в мое время давали задачи, которые не имели математического решения, но ответ необходимо было дать и обосновать "решение". Школьный учитель учил нас к каждой задаче подходить творчески. Именно поэтому очень часто на контрольных работах приходилось видеть с десяток разных решений одной и той же задачи, и все они были правильными. А про олимпиады и говорить было нечего. Там каждая задача была маленьким математическим художеством.

А сейчас... последние 10 человек, пришедшие ко мне устраиваться на работу, не знали, как вычисляется площадь прямоугольника. Подозреваю, что их было больше 10-ти, просто раньше никого не спрашивал. Люди с высшим экономическим образованием не могут посчитать сколько процентов добавить к 100, что бы получить 120. И это не придуманные истории. Это следствие преподавания вот таких училок, которые пытаются втюхать детям понятия о чашках и сахаре, вместо того, что бы объяснить что такое математика и как ее можно использовать для решения числовых задач.

 

-- бред же. И вот почему: ни на каком уровне понимания математики это не важно.

В высших эмпиреях, где умножение уже не обязательно коммутативно, сама формулировка "a * b -- это когда мы берём a и суммируем b раз" неприменима (в частности, потому что для не-натуральных b эта абстракция начинает трещать по швам). А пока речь идёт именно о "низовом" понимании, который нужен в младших классах, совершенно безразлично, какой порядок ставить.

-- Сынок, ты школу умственной коррекции закончил? или из детей фурсенко будешь? Нет множителя и сомножителя в данном случае. Есть множитель и множитель. Страна заселена дебилами ,которые скоро будут утверждать что 3*2 не равно 2*3. Вы что с детьми делаете, безмозглые пидорасы????

-- Я недавно был у друга на стройке, там прораб ржал над строителями, которые спорили, как правильно -- умножать на 0.6 или на 0.60!!!

-- ЕЩЕ РАЗ ДЛЯ ТУПОРЫЛЫХ КУРИЦ ОБЪЯСНЯЮ - ХУЙНЯ, КОТОРУЮ ТРЕБУЕТ ТУПАЯ УЧИТЕЛКА - НЕ ИМЕЕТ РОВНО НИКАКОГО ОТНОШЕНИЯ К РЕАЛЬНОМУ ПОНИМАНИЮ АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ!!!!

Ни с точки зрения физики - ни с точки зрения математики -ни с точки зрения (ТЕМ БОЛЕЕ!!!!) программирования.

 

-- Еще раз: ХУЙНЯ, КОТОРУЮ ВЫ ОТСТАИВАЕТЕ - С ТОЧКИ ЗРЕНИЯ ФИЗИКИ (ЭТО В ПЕРВУЮ ОЧЕРЕДЬ!!!!) ВРЕДНА!!!!

Вредна и никому не нужна и ни один физик или математик или программист или даже простой фермер - НИКОГДА такую с позволения сказать "логику" решения задач - НЕ ИСПОЛЬЗУЕТ!!

дама! вы в математике - нуль, в физике - тоже нуль, так хоть русский язык вы понимаете???

так вот, блять, я вам русским по белому говорю - ИМЕННО и В ПЕРВУЮ ОЧЕРЕДЬ с точки зрения физики и логики решения текстовых задач - училка лепит хуйню - и вы лепите - тоже абсолютную хуйню.

Причем не просто хуйню училка лепит - а хуйню, которая ПРЯМО противоречит специально выделенному разделу в программе математики для младших классов - который называется ЧТЕНИЕ И АНАЛИЗ ТЕКСТОВЫХ ЗАДАЧ

Где - опять же черным по белому написаны требования - уметь выделять из текста существенное и отбрасывать несущественное; уметь переводить предложения вида "столько-то на каждого" - в удельную размерность, а число "каждых" - в безразмерные РАЗЫ!!!

короче. вы - ПОЛНЫЙ НОЛЬ в а) математике; б) физике; c) педагогике и d) АБСОЛЮТНО не знаете образовательные стандарты Российской федерации для младшей школы по математике за второй класс.

Следовательно - заткнитесь уже и молчите в тряпку, дура стоеросовая!!!

Честно говоря, стандарты -- они тоже того-с... См. давнюю статью "ФГОС против образования".

-- Помню, когда я была мелкой (года 4, не больше) у нас в садике начали подготовку к школе или что-то типа того. В общем, учили считать-писать и так далее. И вот, рисует гадкая воспиталка Катерина Васильевна на доске пять солнышек и просит их сосчитать. Я напрягаю свои крошечные мозгёнки и шепчу: "Пять!". И что? Она мне говорит - нет, не правильно! Я: "А сколько тогда?". Она: "Мы еще не прошли число пять, поэтому здесь три солнышка и еще два солнышка, ясно?". Я: "Угу". С тех пор ненавижу математику...

-- Вот у меня есть пример, когда ребенок вообще не дружил с математикой. Как это по условиям задачи мама дала Васе два яблока, а Пете - три. Она что - не мать, как может мать дать детям разное количество яблок.

А еще кошмар: к трем прибавить три. Чего - первое, что спрашивал ребенок. Вот если конкретизировали, не важно чем - машинами, яблоками, ручками, то получалось.

-- "вместо букваря читал постороннюю литературу", ага. Должен буквы учить, а он, понимаешь, Жюль Верна читает. А надо - чтоб как все!

-- Мне в начальных классах снижали оценку за то, что я не отступил ПОЛОЖЕННОЕ количество клеточек от полей или еще что-то в этом роде.

-- Да-да, тоже помню подобное. :) Самое печальное, что при этом совершенно не умели объяснить почему нужно то, что они требуют и почему нарушать эти правила нельзя. Т.е. если бы мне объяснили, что таким образом я учусь делать типовое оформление результатов, которые, в результате, легче и лучше воспринимаются другими (не самое маловажное во взрослой жизни), то я бы, возможно, может даже понял.

Вот согласен. Причём я оставлял эти поля на нужное кол-во клеточек, но их всенепременно надо было провести, причём определённым цветом.

-- И дело не в оформлении задачи. Просто их так учат в педвузах. Представьте себе профессора педвуза. Он всю жизнь учит студентов методике преподапвания математики. При этом он сам с живыми математическими задачами не соприкасается. И его научный руководитель не соприкасался, и научный руководитель его научного руководителя не соприкасался и т.д. Вы представляете, до какой степени за несколько таких поколений утрачивается адекватное восприятие предмета? Вот до такой и утрачивается, что становится важным, в каком порядке числа перемножать. Раньше их как-то удерживали в сознании такие люди, как Колмогоров, Понтрягин. А сейчас они предоставлены сами себе. У них там уже давно выработалась некая "математическая" субкультура. Вот мы знаем, что 9х2=2х9, но высосем из пальца причины, по которым одна запись хорошая, а другая плохая. Вот в этом и состоит суть педвуза, этому учат студентов.

-- У меня была такая же проблема, когда я был учеником. Я отлично знал математику (на интуитивном уровне), в первом классе я освоил всю программу третьего, а в пятом - восьмого. Я был реально лучшим в школе по математике, побеждал в олимпиадах города, занимал призовые места на национальных и международных олимпиадах, закончил МФТИ с красным дипломом.

Меня всегда гнобили учителя математики какими-то мелкими методистскими приколами. В этом конкретном случае я еще в 5 лет понимал, как на что умножать. Я всегда эти условности игнорировал, а мне снижали оценку. Дискриминант считал в уме. Пропускал половину рассуждений - мне казалось не важным все записывать.

Учителя мне пытались доказать, как нужно жить - отчитывали, занижали оценки, выговаривали родителям, объясняли, что я не поступлю в вуз и меня заберут в армию... :)

Сейчас моя профессиональная позиция и три высших образования исключают необходимость кому-то что-то доказывать. Я сам иногда преподаю студентам, наоборот пытаюсь поддержать интеллект, творчество и неординарное мышление.

 

-- Детки - а потом и уже взрослые люди, обучавшиеся по таким методичкам - потом испытывают неимоверные трудности.

Например, уже в вузе таким несчастным совершенно невозможно объяснить, что математика с точки зрения физики - это всего лишь язык, удобный для описания происходящего. И что одна и та же математическая формула может описывать совершенно разные явления - это вообще за гранью понимания людей, намертво с детства привязанных к литрам и чашкам. Формальную логику они тоже не в состоянии освоить - так как никак в толк не возьмут, почему вычисления по формулам логики не зависят от предметного значения выражений.

Не могу не напомнить, что в т.н. диалектической "логике" её адепты именно что оперируют конкретными предметами ("колос отрицает зерно" (с)).

-- Я вам расскажу реальную историю из педагогической практики (я была свидетелем). Жила была девочка - примерная послушная отличница. Всегда пятерочки. Перешла в среднюю школу из младшей - и понеслась. По физике - двойка за двойкой. Слезы, гнев и в конце концов вывод родителей - ой, у нашей девочки гуманитарный склад ума. Через год ее перевели в другую школу, где на физику смотрели сквозь пальцы.

Так вот я тогда - хоть девочка не у меня училась физике - спросила ее учительницу начальных классов. Благо повод попался великолепный. Тетка собиралась затариться двумя мешками картошки по 10 рублей за кило. то есть 16 кг она хотела купить. И об этом в учительской сказанула. И я ее - спросила, приготовила ли она 160 кг картошки, чтобы ее везти продавцу.

Она замерла. То есть как говорит, так? я дескать, деньги повезу. Почему, спрашиваю? ну как же - 16 умножить на 10 = 160 рублей. ДАА??? Чой-та? килограммы на рубли умножаем - значит, получаем килограммы ведь? детей то вы ТАК учите считать, а сами? Сами что - в кусты?

Покраснела. В конце концов от нее избавились - просто попросили уйти по хорошему.

 

-- Почитал комменты. Очешуеть. Какие литропокупатели? Какой, к псам, правильный порядок явно указанных целочисленных величин в элементарном уравнении?!?

Это арифметика, детка. Не основы математического анализа, не векторное исчисление, не алгебра и даже не элементарная математика. Это арифметика для младших классов средней школы. И, кстати, не русский язык, грамматика, основы логики и закон божий.

А арифметика (как раздел математической науки) оперирует абстракциями. И если ребенок смог перевести литры молока (белые, с пенкой, один разлили случайно а два еще украли) и покупателей (взрослый дядька злой был, а бабушке два литра много будет) в числа и дать ответ - то какая к бесам тройка?!?

 

-- на практике эта погоня за строгой бюрократической правильностью оформления и решения просто приводит к тому что люди заучивают - это НАДО решать так, это так. все это превращается в механическую зубрежку и отношение к математике как " это невозможно понять, это надо запомнить".

если что у меня высшее математическое и опыт преподавания, причем уже в техникумах и инситутах. где на учениках очень хорошо видны последствие этой механизации. они не умеют думать, они не понимают почему и что они делают, " нас так научили а так не учили".

Есть очень поучительная и интересная книга: Айрат Димиев, "Классная Америка". Я когда-то на сайте её выложил, но потом библиотеку убрал, да и лишнего там много. Но советую прочесть и приведу отрывок в тему.

Моя собственная дочь по прибытии в Америку пошла в седьмой класс в Johnston Middle School. Это одна из лучших школ. А по математике она была определена в так называемый Advanced Placement (сокращенно АР) класс. Считается, что АР классы для одаренных и увлеченных детей, где предмет преподается по более углубленной программе, нежели в обычном классе. Я очень внимательно следил за её учебной программой. Так вот, то, чем они занимались на уроке математики, было таким примитивом, что я даже не стану утомлять читателя подробностями. Это примерно уровень третьего-четвертого класса российской школы. И это в сильном классе. А что же там делается в обычных?

Более-менее нормальная математика начинается в восьмом классе. Я не оговорился — не алгебра и геометрия, а именно математика, так как никакой алгеброй там ещё не пахнет. Одна из моих российских коллег — Катерина — как раз ведет математику в восьмом классе в Fondren Middle School. По её словам я могу достаточно объективно судить о том, что там делается.

Год начинается с изучения отрицательных чисел, и решаются примеры на уровне:

5 + (–8) = ?

Причем сидят ученики на этом очень долго, так как их воображение отказывается воспринимать отрицательные числа. Как говорит сама Катя, у них нет чувства чисел. Наиболее сложное для них — вычесть отрицательное число:

5 – (–3) = ?

Или сложить два отрицательных:

–5 + (–3) = ?

Решая последний пример, они получают либо 2, либо –2, но только не –8.

После этого начинается изучение дробей и действий с дробями. Наиболее сложным заданием по этой теме является пример типа нижеследующего:

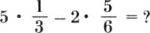
Справляются с этим заданием не более 30 процентов учащихся.

Следующий этап — уравнения. Самые простейшие, типа

25х = 100

Что интересно, они решают такие уравнения не так, как в России. Я сам неоднократно наблюдал это. Мы, чтобы найти х, делим 100 на 25, что кажется нам вполне логичным. Ведь х в 25 раз меньше, чем 100. Американцы делают это гораздо круче. Чтобы найти х, они делят обе части уравнения на 25. В результате слева остается х, а справа 4.

Круто, правда? Это может показаться очень грамотным с математической точки зрения, но совершенно не способствует пониманию учениками сути производимых действий. Они не успевают осознать, что х в 25 раз меньше 100, механически выполняя показанные учителем операции.

Следующий этап — проценты. Около месяца восьмиклассники учатся рассчитывать, сколько процентов составляет, например, 15 от 60. Причем опять-таки делают это чисто механически. Они не делят 15 на 60, чтобы осознать, что 15 составляет одну четверть от 60. Большинство из них и поделить-то это не могут без калькулятора. Просто механически выполняют операции по данному учителем шаблону.

Будучи практически ориентированными, на математике они учатся строить разные графики. Нет, не функции, которые даются не ранее девятого класса. Просто учатся откладывать точки с экспериментальными данными на оси координат. Наиболее сложным является построение так называемого Circle Graph — круга, где процентное содержание составляющих компонент представлено в виде сегментов. Для выполнения этого задания им нужно рассчитать, сколько градусов будет каждый сегмент, путем умножения процентной доли на 360 градусов. Несмотря на очевидную простоту, далеко не все восьмиклассники справляются с этим заданием.

Вся вышеперечисленная программа рассчитана на полгода. Апофеозом этого курса является решение следующего уравнения:

5 (х + 3) – 7 = 3х + 12

Но это, по словам Кати, уже является для них высшим пилотажем, и справляются с этим заданием не более 10 процентов её учеников.

По словам другого нашего общего коллеги — Камиля Сафина, преподающего математику в Fonville Middle School, ни один из его учеников даже при наличии в руках калькулятора не способен ответить на вопрос — сколько яблок можно купить на восемь долларов, если стоимость одного яблока 1 доллар 53 цента. Если бы одно яблоко стоило два доллара, то есть цифры делились без остатка, то ученики знали бы ответ. А вот реальный вопрос с реальными цифрами вводит их в полнейший ступор.

Закончив таким образом обучение в Middle School, ученики переходят в High School, где ещё раз выясняется, что математики они не знают.

Могу поклясться чем угодно, что более половины моих учеников в девятом классе Westbury High School не могли выполнить простейшее действие типа

47 + (–68) = ?

Что касается математики, то программа High School не сильно отличается от программы Middle School. Теоретически самым верхом в обязательной программе по математике являются логарифмы и решение квадратных уравнений. На практике же большинство школ и учителей либо полностью отказываются от логарифмов, либо просто формально объясняют, что это такое.

Когда я в конце учебного года спросил своих учеников одиннадцатого класса, чему равен десятичный логарифм ста, то лишь двое из восьмидесяти опрошенных дали правильный ответ. Это при том, что вопросу предшествовало краткое объяснение, что такое логарифм.

Научиться решать квадратные уравнения среди учеников обычных классов могут процентов 10—20. Как я уже упоминал ранее, таких предметов, как тригонометрия или дифференциальное исчисление, в обязательной программе не предусмотрено совсем.

Наглядно, не так ли? Продолжаем читать мнения о всей этой псевдопедагогической хрени.

-- Привязка математики к конкретным объектам - это одна из самых ужасных вещей, которые только можно придумать.

Потом эти школьники будут не в состоянии умножить 5 ампер на 220 вольт, потому что их учили умножать только молоко на покупателей.

 

-- задача математики (по крайней мере в начальных классах) состоит именно в том, чтобы показать, что задачи - это тоже примеры, и научить воспринимать реальный мир в отвлечённой математической форме.

А ещё я тут придумал хорошую аналогию:

Слова состоят из слогов. И детей часто учат читать именно так, по слогам. Но абсурдно заявлять, что ребёнок, который читает слово целиком - читает его неправильно. Или не понимает сути морфологии или словообразования, или чего бы то ни было. Наоборот, это показывает более глубокие умения человека в чтении. Так же и тут, такие "костыли" как фиксация положения множителей настолько же необходимы, как проговаривание слогов при чтении(хотя возможно это и помогает детям) - но я плохо представляю себе человека, работающего с текстом - но читающего по слогам. Так и в математике их нужно откинуть как можно быстрее.

 

Кстати, я не сталкивался, но слышал, что где-то с перестройки внедряли "фонетическое обучение" письму. Мол, сначала надо тщательно разобраться, как слышится, так и писать. И только потом как-то нарабатывать грамотность.

Как понимаете, если ребёнок привык писать "карова", "агурец" и "йожыг", то объяснять ему потом, что это было всё для обучения, а теперь надо писать "корова, огурец, ёжик" -- очень мило. Надеяться на грамотность впоследсвии - наивно, это надо стирать память и обучать с нуля. При этом обучают даже не фонетической транскрипции (это будет : [j'ожык].), а вообще непонятно чему. Враги народа в прямом смысле.

Не знаю, как сейчас в школах, но кое-где внедряли точно. Я не копал эту тему -- реально страшно...

Подобный подход -- это диверсия против образования (и, соотв., науки). Как и внедрение изучения религий в школу -- "сейчас вы говорим об эволюции, а на следующем уроке о сотворении". У ребёнка ещё нет ни знаний, ни аналитических навыков, чтобы понять "как на самом деле", и естественным выходом для подавляющего большинства будет не стремление понять, а просто вызубрить, чтобы отвязались.

-- учить математике житейскими аналогиями - плохая идея. потому что в математике очень быстро нарастают идеи, которым нет аналогий в житейском окружении. например, умножение не нужно называть "поиском количества предметов, однообразно разложенных в группы", потому что это сразу перестает иметь смысл при умножении дробных чисел. и если для умножения рациональных еще можно родить какую-либо аналогию, то для умножения иррациональных и комплексных - ну никак. ибо иначе сидит этот обучаемый и ноет, "объясните мне это на велосипедах и колесах".

Точно также нужно как можно быстрее уходить от определения синуса через стороны прямоугольного треугольника, потому что это теряет смысл для тупых углов.

 

-- Для начала пару слов о себе: закончила физический факультет МГУ, преподавала физику в вузах и в старшей школе. Зарегистрировалась специально, чтобы от лица преподавателя физики "поблагодарить" некоторых учителей математики в младшей школе.

Так вот. Те люди, которые пишут с чистой совестью в методичках для младшей школы, что размерность результата зависит от положения множителя в произведении - должны гореть в АДУ. Живьем. И вместе с ними - те, кто это детям навязывает.

Потому что после таких вот "если чашки умножать на куски - получатся чашки" - ко мне приходят люди (дети и взрослые) с полностью угробленными мозгами. То есть фактически непригодные для обучения физике.

Переучить их, научить их понимать реальный физический смысл задачи и физический смысл полученного результата - практически невозможно. И в любом случае - это адски, адски, АДСКИ тяжелый труд.

По своему опыту знаю, что пишут такую бредятину и так преподают - те, кто сами физику не усвоили - ни в школе, ни в вузе.

Приведу пример, с чем приходиться сталкиваться при введении понятия размерности и единиц измерения в средней школе.

Вы решили купить 4 кг сосисок. Цена одного кг сосисок - 100 рублей. Вопрос - что и сколько вы принесете кассиру магазина? Килограммы или деньги? и сколько?

Записываем размерности: количество сосисок 4 (кг). цена -100 руб/кг.

Так вот. Детям - после ваших метод обучения в младших классах - сложно понять, что кг*(руб/кг)=РУБЛИ. И что (руб/кг)*кг - это тоже РУБЛИ.

Ладно, сосиски мы не используем; но когда ребенок при вычислении пройденного пути пишет Расстояние = (скорость)*время и записывает размерность результата в виде (м/с) - потому что первый множитель - это СКОРОСТЬ - мне хочется убиться головой об стену.

Но еще больше хочется убить всех вас, граждане учителя младшей школы, которые сами физику не знают и учат, что при умножении литров на людей получаются литры, а при умножении людей на литры - люди!!

Горите в АДУ!

 

-- Дети, конечно, разные! Только умные и сами поймут, что умножение чисел коммутативно (даже если не узнают этого слова), а вот более слабые на всю жизнь остануться с сомнениями на этот счёт. Зачем же их так калечить?

13 лет назад мой средний сын пришёл из школы и сказал, что у него случился конфликт с учительницей. Первый класс, конец сентября. Школа только началась и для ребёнка это очень важное событие в жизни.

- В чём дело? - спрашиваю,

- Она спросила, какие цифры мы знаем. Я поднял руку и ответил: ноль, один, два,..., девять! - А она сказала, что это неправильно и потом похвалила того, кто ответил "ОДИН",, ..."девять", "ДЕСЯТЬ*. Но ведь "десять" - это же не цифра, а ЧИСЛО!

Я, конечно, объяснил ребёнку, что он совершенно прав, мы используем десятичную систему счисления, в которой ровно десять цифр, тех самых, которые он и назвал, используются для записи любых чисел. К сожалению, отношения с этой учительницей и дальше складывались не. радужно. У ребёнка были постоянные замечания, особенно в связи с математикой. В конце второго класса он перешёл в другую школу. Этой весной заканчивает. магистратуру по математике в одном из лучших европейских университетов. Свободно говорит по-французки и по-английски, конечно, по-русски и сносно по-немецки, а эта его учительница, видимо продолжает учить детей, что "десять"- это такая цифра (в обычной десятичной системе счисления). То есть калечит их разум. Причём в первую очередь именно тем, кому со спосбностями не слишком повезло.

Я лично считаю, что учителей, подобных такой вот и той, с какой начался разговор, надо удалять за профнепригодность с волчьим билетом. А с такими методистами поступать как с врагами народа. Если уж учитель вынужден преподавать по такой методичке, то он должен сказать: так и так, от перестановки множителей ничего не меняется, как я вам объяснял, но оформление требуют именно такое.

-- Еще раз - такого рода методисты и учителя - лезут не в свои сани. Заботой о якобы связи с физической реальностью - они как раз детям мозги портят так, что потом добиться понимания "физика - это и есть реальность вокруг" - ОЧЕНЬ сложно.

Реальность - она же вокруг вся. Язык, на котором люди говорят - это ведь тоже реальность.. И что? где вы видели людей, которые говорят своим детям: пойди купи буханки хлеба две. Или - я взяла яблока три. Или - я помыла тарелок пять. Все говорят -купить две буханки. взять три яблока. помыть пять тарелок. Естественное человеческое мышление (которое по сути своей физическое, а не математическое) - так устроено, что думает сначала - сколько взять, а потом - что.

все уравнения в физике пишутся в виде количествоX что - но нет! Во втором классе эту естественную способность надо необратимо сломать чудовищными выдумками про умножение чашек на куски..

 

-- Самое забавное, что в какой то момент (правда, гораздо позже, к тому моменту, к счастью, этот бред с множимыми они забудут, что, кстати, неиллюзорно намекает на его неебическую практическую ценность) детей начнут парить элементарными функциями, начиная с линейных одночленов типа 2х. И тогда таже учительница будет им говорить что НАДО писать именно 2х, х2 НЕПРАВИЛЬНО. И тройки будет ставить за х2. Будет будет. Математический этикет же!

Но - следите за руками - что такое 2х? это икс взятое два раза, это х+х! А раз так, -значит, это х2! Мы же не два берем икс раз! Мы же икс берем два раза! Раз 2 литра, взятые 9 раз - это 2*9, то и икс, взятый два раза - это х2! %))))

Взаимоисключающие параграфы в обучении? ага. это педагогика такая, вы ничо не понимаете. Учитель прав! Всигда! Это логика, детка. Та самая, о которой нам, тем, кто ее изучал, расскажут те, кто о ней ничего не знают.

 

-- Вот в результате такой методики и выучились придурки, которые, даже получив дипломы, убеждены, что размерность произведения определяется по первому множителю. Посмотрите, сколько их в комментариях. Это называется "бомба замедленного действия сработала". Да, а вы сами как считаете: зависит размерность произведения от порядка множителей или нет?

-- это классическая методика, а вы просто невменяемый неуч, как и толпы вам подобных.

Ещё небольшой фрагмент из "Классной Америки":

Основной целью обучения на уровне начальной и средней школы не является выработка каких-либо навыков и умения мыслить. Задача — дать общее представление о материале, суть которого сразу же; после; написания контрольной работы благополучно забывается. Вместо скучного логического мышления ученикам даются игровые шаблоны-схемы, с помощью которых они должны решать те или иные примеры и задачи. Никакого понимания производимых действий при этом нет. Впоследствии для решения другого типа задач им даются другие шаблоны. Эти шаблоны наслаиваются один на другой. В результате в головах обучаемых невообразимая каша, представляющая собой какую-то смесь обрывочных знаний и отдельных кусков всех этих схем-шаблонов.

Например, каждый американский ученик с начальной школы знает поговорку Please Excuse My Dear Aunt Sally. Этот шаблон подсказывает порядок выполнения математических операций. Первое слово please начинается на ту же букву, что и parentheses — «скобки». Это означает: в первую очередь нужно делать то, что в скобках. Далее следует степень, потом умножение, деление, сложение и вычитание. Зазубрил эту поговорку — и никакой тебе скучной логики. При этом они не понимают, что умножение и деление имеют ту же силу. Если они видят пример:

6 ÷ 3 × 5 = ?

то сначала умножат 3 на 5, а потом разделят 6 на 15 и получат ответ 0,4 в строгом соответствии с шаблоном-поговоркой.

Думать же логически и разбираться в задаче они не приучены. Таких любимых нами в детстве задач, как «Из пункта А в пункт Б вышел поезд», в их учебной программе нет совсем. Я очень сомневаюсь, что даже американские ученики старших классов смогут решить такие задачи.

-- А вот интересно, как сторонники 2*9 != 9*2 отнеслись бы к методичке вроде:

В задаче: "У Пети было 3 яблока, Маша отдала ему свои 2, сколько теперь яблок у Пети?" очень важно писать слагаемые
в правильном порядке: 3+2=5, так как иначе получается, что яблоки оказались у Маши?

Примерный диалог в детском саду:

У: ... Итак дети, что мы делаем?

Вася: Складываем!

У: Правильно, Вася, что складываем?

Вася: 2 и 3!

У: Нет, Васенька, ведь у Пети было сначала 3 яблока, а потом мы добавили 2, надо складывать 3 и 2!

 

-- Мы как-то систему разрабатывали. Там были определены несколько стандартных операций на сервере, каждно нужен стандартный набор данных. Например, для регистрации пользвателя (1:имя, 3:пароль, 2:число, 4:адрес, 5:чего-то ещё). Я сервер написал ,который принимает весь стандартный набор целиком. Но клиентскую часть писал Славик. Он принимал все эти данные от пользователя и вместо одного запроса с пятью полями он слал 5 запросов. Это грузило сервер в 5 раз сильнее и злило пользователя, потому что ему вместо 1 секунды (запрос по интернету) приходилось ждать 5 секунд. Я пытался объяснить что бегать в магазин 5 раз глупо, поэтому нормальные люди берут пакет и складывают всё в него. Это понятно даже малым детям.

Но Славик был уже не ребёнок, поэтому действовал чётко по спецификации, в которой было написно, что данные передаются запросами. Он почему-то твёрдо решил, что на один data item нужен 1 запрос. Особую специфику делу придавало то, что славик подстраивался под мою систему, в которой при отправке пакета надо было сразу указывать все 5 предметов. И для того, чтобы вместо одного запроса справится пятью, ему приходилось остальные поля забивать нулями.

Наглдяно, не так ли?

-- Именно следование методикам зачастую и убивает желание учиться у учеников и мыслить не стандартно. До девятого класса я знал и любил химию, а в девятом классе у нас сменился преподаватель на заслуженного педагога России. И на втором же уроке я получил за контрольную три; подойдя к преподавательнице, я спросил почему три -- ведь задача решена верно. Она сказала, что неверно, после 15 минут я ее убедил, что решение верное. Она согласилась, что решение верно, но это ничего не меняет, так как я решил не так, как она рассказывала на прошлом уроке. После этого весь интерес к химии у меня пропал. Ну и скажите, в чем тут великий педагогический смысл -- заставлять учеников решать только данными учителем методами и за шаг в право или лево карать снижением оценок?

Я лично очень благодарен своей учительнице химии. Я в старших классах готовился к поступлению на химфак МГУ, и она мне выдала свои книги для поступления нормального уровня: Некрасова, Реми, ещё какие-то, и честно сказала, что сама она поступала давно, с ходу на любой вопрос уже ответить не сможет, но если что будет непонятно, то обращаться -- и будем разбираться вместе. При этом на уроках не требовала делать что-то по стандартной программе, кроме формальных контрольных для отчётности.

-- Вспомнился известный исторический анекдот о Гауссе. Кто такой Гаусс? Всего лишь один из самых известных математиков в истории. Многими специалистами считается одним из самых продуктивных математиков, задавший основы более чем сотни различных математических областей.

Так вот, когда Гаусс был в школе, он уже тогда был башковитым и доставал учительницу вопросами. Чтобы занять чем-то этого надоедливого задрота, училка задала Гауссу задачу посчитать сумму всех целых чисел от 1 до 100, думая, что уж это-то займет его надолго. Однако не прошло и минуты, как Гаусс обьявил, что готов. Как он это сделал? Вместо того, чтобы считать числа тупо подряд, он заметил что их можно разложить по парам - 1 и 100, 2 и 99 и так далее. Сумма в каждой паре равна 101, а всего пар 50 штук - от единицы до 50. Значит сумма 50*101 (ой, или 101*50? все никак не запомню как ПРАВИЛЬНО %) ).

Что скажет на эти училка из поста и поддерживающие ее комментаторы? Тройбан тебе, Гаусс, в лучшем случае. Сказано же тебе, тупица, русским немецким языком, посчитай от 1 до 100. вот так - 1+2+3+4+5+....+100 и только так. Только в таком порядке. Как в методичке. Неуч, сразу видно - фошист.

 

-- Знаете, что такое шоры?

Это такие щитки (наглазники), которые надевают на морду лошади по бокам, чтобы она смотрела только вперед – и никуда не сворачивала.

Во вступительной статье к изданию своих сочинений автор (притом – высокоученый) написал что-то о НАРОДНЫХ РУССКИХ ПЕСНЯХ.

И была у нас в издательстве такая противная баба, в должности литературного корректора.

Которая, натурально, тут же исправила «народные русские песни» на русские народные песни.

(При этом она пропустила другие неточности в тексте, действительно существенные, в то время как в формулировке автора ошибки нет никакой.)

Просто она привыкла к шаблону.

Бывают РУССКИЕ НАРОДНЫЕ ПЕСНИ – и «НАРОДНЫХ РУССКИХ ПЕСЕН» быть не должно.

Потому что – куриные мозги.

Ну и ещё кусочек "Классной Америки":

Вместо логического мышления дети в школе обучаются играм и манипуляциям. Они на сравнительно короткий срок (как правило — до конца урока, в лучшем случае — до ближайшей контрольной) обучаются простым операциям-схемам, суть которых — что куда и как перенести или передвинуть. Вот, например, как их учат переводить метры в сантиметры.

Перед учениками шкала, на которой расположены приставки единиц измерения, начиная от меньших слева, заканчивая крупными справа: милли, санти, деци, один, дека, гекто, кило

Каждой единице соответствует ячейка. Таким образом, между метром и сантиметром две ячейки. Чтобы превратить, например, 5,372 метра в сантиметры, нужно перенести запятую на две ячейки. Теперь самое главное — нужно решить, в какую сторону переносить. Инструкция такова — все время переноси в сторону, обратную движению. По нашей шкале от метров к сантиметрам мы движемся справа налево, значит, запятую нужно перенести слева направо. Получаем 537,2 см. Осознать, что в метре 100 см и соответственно значение, выраженное в см, будет в сто раз больше, для них слишком сложно. Очень немногие могут понять это и использовать на практике.

Читатель мне не поверит, но большинство учеников 11-го класса постоянно путаются, переводя граммы в килограммы и наоборот. Если они перепутали, в какую сторону перенести запятую, то вполне могут написать:

34,5 г = 34500 кг

совершенно не смутившись полученным результатом.

Так они и переносят знаки слева направо и справа налево, не понимая смысла выполняемых операций. Учителя даже и не пытаются объяснить студентам, в чем их истинный смысл. Отчасти потому, что многие учителя в свое время сами обучались по подобным методикам.

Для лучшего усвоения материала учителей принуждают использовать «передовые методы обучения». Суть одного из них, на презентации которого мне пришлось побывать, заключается в том, что, совершая вышеописанное действие, ученики одновременно совершают физические движения. Они хлопают в ладоши, прыгают, трясут вытянутыми вверх руками и в одном случае (при делении), приседая, опускают вниз левую руку, а в другом — правую. Очень хорошо делать это все под музыку. Здорово? Здорово! Если бы не одно обстоятельство. Все это происходит не в детском саду и даже не в начальной школе. Такие методики навязываются на всевозможных тренингах учителям средней школы.

Часть третья, Кравецкий: "Учитель, обучи себя"

Как мы видим, грамотный педагог-методист, кстати, получатель целого набора грантов, показывает потенциальным учителям потенциальных учеников правильную последовательность действий для решения определённого сорта задач.

Хорошо ли это или плохо? Многие подумают, что это плохо — ну, поскольку очень плохо давать последовательность действий, которая, как и сопутствующие ей разъяснения, искажает смысл стоящей за всем этим теории, противоречит будущему материалу предмета, да и собственным же предыдущим абзацам. Однако всё не так.

На самом деле методист приучает детей к суровым реалиям мира. Ведь и в дальнейшем им будут даваться нелогичные, противоречивые и антинаучные инструкции, которые в обязательном порядке надо будет выполнять. Эти инструкции напишут соседи учеников по парте — тоже мастерски подготовленные к жизненным реалиям, — а то и сами эти ученики. Если бы они учились так, как, например, я, им бы очень тяжело пришлось в подобного рода случаях, благодаря же приведённой на скриншотах методике они будут к ним подготовлены. Столь ценный навык нельзя переоценить: ведь чем меньше логики в используемых методах, тем лучше работается над душой. Поэтому я выражаю своё всецелое одобрение данному подходу...

Счёт палочек иллюстрирует абстракцию, а не заменяет её собой. И тут крайне важно добиться именно понимания абстракции на примерах, что, к счастью, детям даётся в некотором смысле даже проще, чем в своё время не понявшим абстракции взрослым.

В этом плане первое, что должно закрепиться в голове у детей: результат умножения — один и тот же, независимо от способа, которым мы его получили. Мы можем просуммировать a раз второй множитель, можем b раз просуммировать первый, можем a раз взять b палочек и пересчитать их, можем даже набрать и пересчитать палочки моим извращённым способом, но каждый раз мы получим один и тот же результат. И каждый вариант подсчёта будет правильным. Потому что они — суть частные случаи некоторой абстрактной операции.

Пользуясь аналогиями, когда ребёнка обучают слову «стул», ему показывают разные стулья (в том числе, нарисованные), а не один и тот же, запрещая ему назвать «стулом» хоть что-то, кроме вот этого конкретного стула.

Если некто, по примеру педагога-методиста, чьему перу принадлежит текст со второго скриншота, или же по примеру преподавателя с первого скриншота настаивает на том, что варианты неэквивалентны, то он приучает ребёнка к совершенно неправильному пониманию математики. Это нельзя оправдать «простотой изложения» или чем-то подобным: это просто ложная информация. Это вбивание в голову вредного, что потом следующим учителям придётся из головы мучительно выбивать. И хорошо ещё если такие найдутся.

... У профессора-методиста свой путь. В своих рассуждениях он вводит размерность «куски», размерность «чашки» и странное правило, что при умножении размерных величин результат имеет размерность первой.

В математике мы бы имели: 2 кус • 5 чаш = (2•5) (кус•чаш) = 10 кус•чаш

Но согласно пониманию методиста, ни фига, всё не так. Он думает, что 2 кус • 5 чаш = 10 кус; 5 чаш • 2 кус = 10 чаш

Ты, ученик, не можешь найти логику? А нефиг её искать! Есть инструкция — выполняй. Будь готов к тому, что в военное время синус может достигать трёх!

...Кому-то кажется, что строго заданная последовательность операций помогает ученику на первом этапе лучше понять суть решения задач? Вполне возможно. Проблема не в этом. Проблема в том, что здесь мы наблюдаем подход, противоречащий дальнейшему курсу математики, лишённый внутренней логики, вводящий свои идиотские законы проведения операций с размерностями и свои частные определения. Вдобавок в рамках этого подхода отвергаются совершенно верные решения и их результаты. Чему такой подход помогает? Какому такому «пониманию»?

Это — «новый, прогрессивный способ объяснять»? О нет, пишите честно: это способ подготовить детей к жизни в суровом мире, где уровень научного знания среди широких масс уже откатился к девятнадцатому веку. Если не дальше.

См. текст целиком.

2030 год. Учительница и Вовочка.

-- Вовочка, ты решил задачу про фермера?

-- Да, Марь Ивановна.

-- Ну и какой ответ?

-- 18 литров.

-- Каким образом? Как ты умножал?

-- 2х9, как вы учили.

-- А сложением проверял?

-- Да. 2+2+2+2+2+2+2+2+2, как вы учили.

-- И больше ничего не делал?

-- Нет.

-- Садись, двойка.

-- Почему, Марь Ивановна?

-- По новому регламенту во время счета, чтобы не ошибиться, надо еще и пальцы на руках загибать.

 

Часть четвёртая, Akhceloo: "Задача для методиста Игрекова"

 

Люди добрые!!! Не нужно! Вот не нужно вводить несуществующие размерности, вроде "[кусок сахара]", "[чашка]" и "[(кусков сахара)/чашку]" (кратко "[кусков/чашку]"). Понятие "Размерность" имеет смысл ТОЛЬКО для физических величин. Масса, длина, время - и их производные величины. Сила, скорость, энергия... Но не "чашка" или "кусок сахара". В таких дурацких размерностях - нарушается главный принцип: размерность НЕИЗМЕНННА, и не может зависеть от манипуляций с объектом. Иначе, если мы вводим такие искусственные размерности, как "[кусков/чашку]", то Мы будем вынуждены постоянно ПОДГОНЯТЬ размерность объекта в зависимости от способа решения задачи. Для иллюстрации этого разберём следующий пример:

 

Условие:

Дано: есть методист Районного отдела образования (или как их там теперь величают) по фамилии Игреков. Методист Игреков уверен, что все величины в задачках для детей имеют размерности.
Методисту Игрекову на день рождения подарили несколько фарфоровых чашек.
Жена методиста поставила их на стол, и в каждую чашку положила по два куска сахара. Сахар она брала из сахарницы, куда в начале вечеринки она насыпала 50 кусков сахара.
Методист Игреков случайно толкнул стол, и несколько фарфоровых чашек чашек упало и разбилось. Остальные чашки остались на столе.
Жена методиста Игрекова веником подмела осколки вместе с кусками сахара, и выкинула их в мусоропровод.
Оставшиеся на столе чашки жена вымыла, и поставила в шкаф, где было много старых чашек, отличить новые чашки от старых невозможно.
Сахар она не стала класть обратно в сахарницу, а сложила в два полиэтиленовых пакетика.
Методичный методист Игреков сосчитал, сколько сахара у него осталось. Оказывается, в сахарнице осталось 30 кусков сахара. Через прозрачный полиэтилен пакетиков видно, что в каждом пакетике лежит по 5 куска сахара, всего - два пакетика.
Как методисту Игрекову узнать, сколько чашек разбилось?
Сколько чашек разбилось?

Методист Игреков начинает решать задачу.

Было 50, по условию задачи осталось 30 в сахарнице.

Ага.

Чтобы узнать, сколько сахара в пакетиках, методист умножает:

5[кусков/пакет] * 2[пакета] = 10 [кусков] (сахара).

 

После этого он приступает к вычитанию: 50 [кусков] - 30 [кусков/(в сахарнице)]....

Постойте, говорит методист. Мне известно, что мы не можем складывать величины разных размерностей.

Выложим куски сахара из сахарницы на стол. Теперь они из 30 [кусков/(в сахарнице)] превратились в 30 [кусков], теперь их можно складывать и вычитать.

Кстати, попутно вопрос: а почему размерность кусков сахара теперь стала 30 [кусков]? Куски же лежат теперь на столе. Не логично ли было написать: 30 [кусков/(на столе)]? А то вдруг нам потом придётся умножать на число столов? Но оставим этот вопрос для самостоятельного изучения нашим ученикам.

Теперь методист Игреков может выполнить вычитание:

50 [кусков] - 30 [кусков] - 10 [кусков] = 10 [кусков] (пропало, жена выкинула в мусоропровод вместе с чашками)

По условию задачи, в начале вечеринки жена методиста разложила сахар по 2 [куска/чашку].

Делим 10 [кусков]/(2 [куска/чашку]), вспоминаем правила деления дробей, и получаем, что размерности "кусок" сократились, и осталась размерность "чашка":

10 [кусков]/(2 [куска/чашку]) = 5 [чашек] упало на пол.

 

Ладно. Справился.

Теперь усложним условие задачи.

Жена методиста Игрекова положила сахар не в два полиэтиленовых пакета по 5 кусков в каждом.

Жена методиста положила в один полиэтиленовый пакет 4 куска сахара, а в другой - 6 кусков. Через прозрачную плёнку прекрасно видно, сколько в каждом пакете сахара.

Что делать бедному методисту Игрекову? Теперь уже нельзя умножать.

По идее нужно складывать. Как мы помним из предыдущего решения задачи, сахар в пакетах измеряется в единицах "[кусков/пакет]":

4[кусков/пакет] + 6[кусков/пакет] = 10[кусков/пакет]

Э, нет. Так не пойдёт. Мы ничего не умножаем, как же нам теперь избавиться от [ /пакет] в знаменателе размерности?

Подумав, методист находит выход:

Нужно высыпать сахар из пакетов на стол. После этого сахар из единиц 4[кусков/пакет] + 6[кусков/пакет] превратится в сахар в единицах

4[кусков] + 6[кусков], и мы можем спокойно получить 10[кусков] в сумме. Хотя, может быть, не 10[кусков], а 10[кусков/(на столе)]? Нет, не будем думать о столах...

 

Ладно, снова справился. Казалось бы, хвала методисту Игрекову?

Не тут-то было!

Ещё раз усложним условие задачи. Один из пакетов с сахаром (тот самый, в котором 6 кусков сахара) жена методиста Игрекова завязала так, что развязать методист Игреков не может. Полиэтилен очень прочный, разорвать пакет Игреков тоже не может. Ножниц у методиста Игрекова нет, в общем, не может он высыпать сахар из этого пакета на стол. В то же время через прозрачную плёнку прекрасно видно, что в пакете лежит 6 кусков.

И что?

Методист Игреков теперь не может решить задачу.

Если он начнёт складывать куски в пакетах, у него получится не та размерность:

4[кусков/пакет] + 6[кусков/пакет] = 10[кусков/пакет]

Если он высыпал 4 куска сахара из первого пакета, то он вообще не имеет права складывать величины разных размерностей:
4[куска] + 6[кусков/пакет] - НЕЛЬЗЯ СКЛАДЫВАТЬ (ну, методист же считает, что это величины разных размерностей!)

Высыпать сахар из второго пакета методист не может - не получается развязать пакет.

По мнению методиста Игрекова, теперь задача не имеет решения.

:))))

 

Кстати, какой ужас бы получился, если бы методист Игреков стал в начальной задаче не умножать, а складывать!

Смотрите, всё ведь так хорошо было:

5[кусков/пакет] * 2[пакета] = 10 [кусков] (кусков сахара)

А если складывать:

5[кусков/пакет] + 5[кусков/пакет] = 10[кусков/пакет] - размерность не та...

Получается что заменить операцию умножения операцией сложения мы не можем!

А как же определение операции умножения?

Всё, методист Игреков окончательно зашёл в тупик.

 

Часть пятая, всякие дополнения и мысли

 

Математика -- это язык науки, без её освоения никакого развития науки, техники и даже психики не будет. И чем раньше индивид усвоит абстрактное мышление, тем лучше. Т.е. всякие куски/чашки должны сразу же переводиться в абстрактные числа и перемножаться в любом порядке. Потом, когда в физике станут важны размерности, они добавятся естественным образом. И не будет проблем с векторами, матрицами, комплексными числами и проч., -- их в виде кусочков сахара уже не особо изобразишь.

Однако, помимо нормальных людей, есть дебилы. Которые вообще никогда не поймут ничего выше уровня "разложить сахар по чашкам" -- у них конкретное, предметное мышление, к абстрагированию они не способны. Простейший текст на умственное развитие -- попросить объяснить смысл пословицы, образного выражения и т.д.

Так вот, метод обучения "строго таким образом, и никак иначе" -- это для дебилов. Систему они не поймут, поэтому в порядке хоть какой-то социализации их учат выполнять действия строго определенным образом (к тому же их часто нервирует неопределенность, выбор им сделать трудно). Что-либо с размерностью они тоже считать не будут. Им прививают не знания (понимание), а навыки.

И вот этот-то метод для дебилов навязывают нормальным детям, сбивая им нафиг абстрактное мышление (впрочем, "тогда получатся чашки" -- это полный дебилизм в любом случае). Это всё равно как обучать работе в MS Word методом "кликни два раза мышкой на таком-то значке на рабочем столе", "регулярно нажимай Ctrl-S", "если нужно сделать курсив -- используй мышку и кнопку на панели, и никак иначе", "выравнивать пробелами", "стили -- а что это такое? не надо этого знать" и т.д.

 

На собеседовании в школе для особо одарённых детей шестилетнего Вовочку попросили рассказать, чем автобус отличается от троллейбуса.

Вовочка ничего скрывать от тёти не стал и честно ей сообщил, что автобус работает на двигателе внутреннего сгорания, а троллейбус - на электродвигателе переменного тока.

Оказалось - ничего подобного!

Просто троллейбус с рогами, а автобус - без.

И нечего тут морочить тёте голову!

 

vladislav03:

ПС: А потом у этих же людей на укроине фофызма нету, ибо президент еврей

ПСС: И да, переход от формализации к упрощению "для чайников" - это одна из причин дебилизации образования. Самостоятельный переход от конкретного к общему, с выделением закономерностей и оформлении конечной идеи, для обывателя не просто нетривиальная задача. Большинство обывателей на это неспособны вообще. Именно поэтому масс-медиа сейчас разжёвывают абсолютно всё - потребителю не только лень поработать мозгами, у него сам процесс вызывает отторжение.

Обращали внимание на стандартную ошибочную запись "КВт/ч"? Люди даже не задумываются, что это значит, и привычно вместо умножения пишут деление. Мелочь какая.

Типичные фразы разговора "на умную тему и с понтами":

" Параллельные прямые ПЕРЕСЕКАЮТСЯ в бесконечности. При всей твоей наглости, прямо заявить, что это не так, духу у тебя не хватило, что не удивительно. Но ты мог бы сослаться на то, что бесконечность - это бесконечно далеко и поэтому её как бы и нет. Поэтому я тебе сразу и намекнул на сингулярность, показывая, что бесконечность, вообще-то, может оказаться совсем рядом. Но ты ж мало того, что намёка не понял, ты вообще ничего не понял".

"...гражданин, параллельные прямые не пересекаются только на плоскости. на сфере и седле - пересекаются, и еще как".

"нет такого хфундаментального свойства у параллельных прямых. как ведут себя параллельные прямые - пересекаются они или нет - зависит от выбранной системы аксиом, описывающей определенную поверхность. а ваще то наше пространство неевклидово, так шта.. сами понимаете".

 

И это при том, что параллельные прямые НЕ пересекаются по определению параллельности как термина!

В аксиоматике Лобачевского пятый постулат таков: "На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную". А в аксиоматике Римана через такую точку нельзя провести к прямой ни одной параллельной..

-- Я помню, когда в Бауманке учился, там один препод по термеху рассказывал, что существуют студенты, которые могут запомнить все задачи из учебника, но при переворачивании схемы (все силы оставались те же, все рычаги/расстояния тоже) впадают в ступор. Мне тогда бредом казалось - на хера столько учить, если можно чуть-чуть понять и запоминать надо будет в сто раз меньше? А потом увидел, что и правда, есть такие.

Яблоко с подвохом

Несколько раз во вредленте за последние дни пробегали подборки задачек "с подвохом". Как правило, отгадки довольно просты. Но одна задачка озадачила.

Вот она (оставим литературно-филологические характеристики текста на совести автора:)

На одном острове стоит яблоня с мальчиком, а на другом — больница с бабушкой. Между островами мост. Мальчику надо принести бабушке 2 яблока, но мост выдерживает только одного мальчика и одно яблоко. После того, как мальчик пройдет, мост разрушится. А в воде водятся акулы. Как ему перенести яблоки?

Решить я не смог. Решил погуглить. На форумах предлагалось множество бредовых идей. Например, что надо одно яблоко катнуть по мосту (следовало разъяснение, что мост слишком длинный) или что мальчику надо снять одежку и вместо нее нести второе яблоко (следовало разъяснение на грани 242 статьи - мол, мальчик и так уже голый). Еще предлагали сорвать все яблоки с яблони, накормить акул, и, пока они едят, плыть с острова на остров...

Потом я увидел правильный ответ.

Он такой: Мальчик должен идти по мосту и жонглировать двумя яблоками.

И я понял, что наверное я не изучал в школе физику и не знаю, что такое импульс силы. И не изучал в институте сопромат - и не представляю, что такое динамическое нагружение. Или автор задачки это не изучал?

Из комментов:

Такое "решение" задачи не зависит от n - числа яблок. Если бы мальчик мог жонглировать сорока яблоками, то перенес бы и сорок. Остается сконструировать полутонный грузовик, подкидывающий сорок полутонных грузов и легко перевозящий двадцать тонн.

 

И замечание строго по сути феномена:

Автор ответа, наверное, юрист. Формально у мальчика в любой момент не более одного яблока - условие выполнено. Реально средняя нагрузка на мост будет та же, плюс превышение для компенсации сопротивления воздуха при броске яблока вверх (пренебрежимое), плюс динамические нагрузки в момент броска (уже не пренебрежимые). Естественно, при попытке устроить такое шоу на непрочном мосту шанс рухнуть резко растёт. Решить задачку в реале без подручных средств нельзя. А если есть хотя бы кусок картона или тряпка большая - то уже проще. Делаем крыло типа воздушного змея и с ним бежим. Подъёмная сила всяко скомпенсирует два яблока. Правда, динамические нагрузки от бега опять же.... В общем, нефиг на такой мост вообще вылезать. А бабушка пусть лучше рыбу ловит, в ней тоже витамины.

Ишшо методичка

Данный пример на стр. 158, переместительный закон на стр. 22, что характерно.

(Государственный педагогический институт им. Герцена, И.Н.Кавун, Н.С.Попова,"Методика преподавания арифметики. Для учителей начальной школы и студентов педтехникумов" Допущено Наркомпросом РСФСР, 1934 год)

В тему:

"В 1931-35 гг. была разработана новая программа по математике для начальных классов, отличительными особенностями которой были строгая система в расположении учебного материала, точно очерченный круг знаний, умений и навыков, равномерное распределение учебного материала по годам обучения. В программе значительное место отводилось обучению разного рода жизненных задач, возникающих в практике хозяйственной деятельности. При этом меньше значения придавалось сознательному восприятию способов решения этих задач. Многие из них решались по заучиваемым формулам, с помощью громоздких и во многом искусственных приемов. Большое значение придавалось вооружению учащихся практическими умениями и навыками, связанными с выполнением измерений на местности ".

ifc, Мамкины беззаботники призывают Апокалипсис

https://ifc.livejournal.com/1241820.htm

"Новый ‎опрос ‎Yahoo ‎News/YouGov ‎показал, ‎что, ‎когда ‎американцы‏ ‎узнают, ‎что‏ ‎на‏ ‎самом ‎деле‏ ‎будет ‎означать ‎бесполётная ‎зона ‎НАТО‏ ‎над ‎Украиной‏ ‎(а‏ ‎она ‎будет ‎означать‏ ‎"сбивать ‎русские‏ ‎самолёты"), ‎поддержка ‎данной ‎меры‏ ‎падает‏ ‎с ‎40‏ ‎до ‎23‏ ‎процентов. ‎Недавние ‎опросы ‎показали, ‎что‏ ‎многие‏ ‎поддерживают ‎эту‏ ‎меру, ‎а‏ ‎СМИ ‎буквально ‎одержимы ‎продвижением ‎её‏ ‎(хотя‏ ‎она‏ ‎может ‎легко‏ ‎привести ‎к‏ ‎началу ‎Третьей‏ ‎мировой‏ ‎войны). ‎Однако ‎если‏ ‎респондентам ‎говорят, ‎что ‎это‏ ‎по ‎сути‏ ‎означает‏ ‎войну ‎с ‎Россией ‎- ‎противники ‎бесполётной ‎зоны ‎удваиваются‏ ‎и ‎составляют‏ ‎43%".

В‏ ‎этой ‎новости ‎на‏ ‎свой ‎лад‏ ‎великолепно ‎(ибо ‎великолепным ‎может ‎быть‏ ‎и‏ ‎абсурд) ‎всё ‎- ‎начиная ‎от ‎опрашиваемых ‎и ‎заканчивая‏ ‎опрашивающими.

Перед ‎нами‏ ‎наглядный‏ ‎идиотизм ‎современности‏ ‎в ‎полный ‎рост, ‎без ‎одежды‏ ‎и ‎в‏ ‎максимально‏ ‎непристойной ‎(хотя ‎и‏ ‎красноречивой ‎на‏ ‎свой ‎лад) ‎позе. ‎

1)‏ ‎Гордые‏ ‎современники ‎высказывают‏ ‎свою ‎вескую‏ ‎поддержку ‎сущности, ‎о ‎содержании ‎которой‏ ‎в‏ ‎действительности ‎не‏ ‎имеют ‎ни‏ ‎малейшего ‎представления;

2) ‎Профессиональные ‎опросчики, ‎могучие‏ ‎социологи‏ ‎и‏ ‎знатоки ‎Общественного‏ ‎Мнения, ‎тем‏ ‎не ‎менее‏ ‎изучают‏ ‎данный ‎детсад ‎и‏ ‎делают ‎вид, ‎будто ‎они‏ ‎имеют ‎дело‏ ‎действительно‏ ‎с ‎мнением ‎и ‎действительно ‎общественным ‎- ‎а ‎не‏ ‎с ‎жалким‏ ‎результатом‏ ‎работы ‎многолетней ‎фабрики‏ ‎согласий;

3) ‎И‏ ‎при ‎этом ‎речь ‎идёт ‎не‏ ‎о‏ ‎чём-нибудь, ‎а ‎о ‎ядерной ‎войне. ‎О ‎возможности ‎ядерной‏ ‎войны, ‎прикрытой‏ ‎всего-навсего‏ ‎нелепым ‎эвфемизмом.‏ ‎

Мы, ‎разумеется, ‎не ‎можем ‎не‏ ‎высказать ‎несколько‏ ‎мыслей‏ ‎о ‎тех ‎23%‏ ‎американцев, ‎которые‏ ‎полагают, ‎что ‎идея ‎ядерной‏ ‎войны‏ ‎с ‎Россией‏ ‎очень ‎даже‏ ‎ничего ‎(полагая, ‎глядя ‎на ‎вырастающие‏ ‎на‏ ‎горизонте ‎ядерные‏ ‎грибы, ‎эти‏ ‎кретины ‎сказали ‎бы, ‎что ‎их‏ ‎забыли‏ ‎предупредить,‏ ‎что ‎война‏ ‎будет ‎ядерной‏ ‎и ‎что‏ ‎русские‏ ‎тоже ‎могут ‎в‏ ‎нас ‎попасть, ‎и ‎потребовали‏ ‎бы ‎вернуть‏ ‎всё‏ ‎как ‎было). ‎

Но ‎да, ‎ув. ‎друзья ‎- ‎мы‏ ‎живём ‎в‏ ‎мире,‏ ‎где ‎почти ‎половине‏ ‎населения ‎самой‏ ‎передовой ‎страны ‎западного ‎полушария ‎не‏ ‎приходит‏ ‎в ‎голову ‎уточнить, ‎что ‎скрывается ‎за ‎предлагаемой ‎им‏ ‎к ‎поддержке‏ ‎сущностью.‏ ‎Четверти ‎-‏ ‎не ‎хватает ‎даже ‎прозрачного ‎намёка,‏ ‎потому ‎что‏ ‎они‏ ‎не ‎привыкли ‎понимать‏ ‎намёки. ‎

И,‏ ‎наконец, ‎тем, ‎кто ‎их‏ ‎опрашивает‏ ‎- ‎даже‏ ‎не ‎представляется‏ ‎постыдным, ‎что ‎они ‎занимаются ‎заведомым‏ ‎напёрсточничеством,‏ ‎из ‎которого‏ ‎вымыто ‎всякое‏ ‎подобие ‎честности. ‎

...Должен ‎признаться, ‎что‏ ‎если‏ ‎и‏ ‎существует ‎на‏ ‎планете ‎нечто,‏ ‎что ‎никогда‏ ‎не‏ ‎перестанет ‎изумлять ‎любого‏ ‎мыслящего ‎ув. ‎современника ‎-‏ ‎то ‎это‏ ‎невероятный‏ ‎и ‎немыслимый ‎уровень ‎самонадеянного ‎легкомыслия ‎подавляющего ‎большинства ‎окружающих,‏ ‎как ‎коллективного,‏ ‎так‏ ‎и ‎персонального".

Из учебника (!) по логике (!!!)

Евгений Архипович Иванов. Логика: Учебник. – 2-е издание, переработанное и дополненное. – М.: Издательство БЕК, 2002. – 368 с. ISBN 5-85639-280-9 (в пер.)

"Определение не должно быть только отрицательным. Это означает, что в определении могут быть отрицательные признаки, но ими нельзя ограничиваться. ...Нарушение этого правила означает логическую ошибку, которая называется «определение только отрицательное». Например: «Атеизм есть отрицание Бога». Надо добавить: «и утверждение бытия человека на Земле»".

Сцуко!

Во-первых, атеизм -- это неверие в богов, а не "отрицание Бога".

Во-вторых, какое отношение к атеизму имеет "утверждение бытия человека на Земле"?!

 

Ещё, (с) не стоит.

"Определение не должно быть отрицательным.

Определение должно указывать на то, что представляет собой предмет, а не на то, чем не является предмет. Поэтому такое определение, как «свет есть отсутствие темноты», не может дать никакого знания о природе света.
Однако в некоторых случаях определение может содержать в себе отрицание. Например, в определении инертных газов (аргон, неон и др.) указывается их химическая неактивность.

Отрицательные определения употребляются также в тех случаях, когда определяемым является отрицательное понятие. Например: «Иррациональное число — это число, которое несоизмеримо ни с единицей, ни с её частями»".

 

С чего бы это химическая инертность -- отрицание чего-то там?

С какого бодуна иррациональное числе -- отрицательное понятие? Иррациональные числа -- это действительные, но не рациональные. При чём тут произвольные части единицы -- уму непостижимо.

Я понимаю ещё, когда люди лажают на чём-то сложном, типа той же теоремы Гёделя. Но лажать на базовом понимании гносеологии, при этом ещё и учебники писать!!!

Намеренное навязывание зубрёжки

Важно понимать, что это всё -- не случайно, а системно. В разных местах, разными методами, но -- именно что намеренное отучение желания у детей мыслить и познавать.

Вспомним, что было на задней стороне тетрадей в клеточку в СССР:

Удобнейшая форма представления таблицы Пифагора. Сразу понятно, что 2х9=9х2.

А вот вам, казалось бы, почти то же самое. Более поздний вариант, 2007 год.

Вот кем надо быть, чтобы справляться с таблицей при умножении на 1 и на 10?!

Это также означает, что нет понимания смысла умножения в принципе. Если и так не понятно, почему Nх1=N и приходится в таблицу заносить.

А вот закономерный результат:

Мало того, что х1 и х10 предлагается запоминать, так ещё и нагляднейшая форма представления заменена на просто перечисление. Зубрите, детки. Ищите отдельно 2х9 и 9х2 -- почему это одно и то же, в такой форме ничего не намекает.

А вот квинтэссенция современного подхода:

Как эти уродливые головастики способствуют пониманию таблицы умножения? Вопрос риторический...

Зато дебилы могут рассматривать картинки!

Школьная домашка по математике в Миссури, 18+.

y = x + 2
3x + 6y = 12

Ангела была изнасилована маминым _____ в возрасте 8 лет, что определило выбор ею профессии и подтолкнуло к карьере писателя

a. (0,2) бойфрендом

b. (4,6) братом

c. (-3,-1) отцом

x = y – 1
y = -4x + 21

Воспитывая сына одна, эта мать одиночка подрабатывала сутенершей, проституткой и _______

a. (-3,-2) букмекером

b. (9,10) драгдилером

c. (4,5) танцовщицей в ночном клубе

Без комментариев.

Разрыв между умными и глупыми нарастает

https://www.rosbalt.ru/main/2013/12/04/1207437.html

Статья 2013 года ещё. Руководитель лаборатории социальной психологии СПбГУ, глава центра «Диагностика и развитие способностей» Людмила Ясюкова также более двадцати лет работает школьным психологом. В интервью «Росбалту» она рассказала о результатах мониторинга интеллектуального развития школьников и студентов.

-- ...Обобщив, понятийное мышление можно определить через три важных момента. Первый - умение выделять суть явления, объекта. Второй - умение видеть причину и прогнозировать последствия. Третий - умение систематизировать информацию и строить целостную картину ситуации.

Те, кто обладает понятийным мышлением, адекватно понимают реальную ситуацию и делают правильные выводы, а те, кто не обладают… Они тоже уверены в правильности своего видения ситуации, но это их иллюзия, которая разбивается о реальную жизнь. Их планы не реализуются, прогнозы не сбываются, но они считают, что виноваты окружающие люди и обстоятельства, а не их неправильное понимание ситуации.

Степень сформированности понятийного мышления можно определить с помощью психологических тестов. Вот пример из тестирования детей шести-семи лет, с которым не всегда справляются и взрослые. Синица, голубь, птица, воробей, утка. Что лишнее? К сожалению, многие говорят, что утка. У меня были недавно родители одного ребенка, горячились, доказывали, что утка – правильный ответ. Папа – юрист, мама – учитель. Я им говорю: «Почему утка?» А они отвечают, потому что она большая, а птица, птичка это, по их мнению, что-то маленькое. А как же страус, пингвин? А никак, у них в сознании закреплен образ птицы как чего-то маленького, и они полагают свой образ универсальным.

-- И какой же процент наших соотечественников умеет выделять суть и видеть причинно-следственные связи?

-- По моим данным и по данным других исследователей, меньше 20% людей обладают полноценным понятийным мышлением. Это те, кто изучал естественные и технические науки, научился операциям выделения существенных признаков, категоризации и установления причинно-следственных связей. Их, однако, среди принимающих решения о развитии общества мало. Среди политических консультантов у нас психологи, философы, неудавшиеся педагоги – люди, у которых с понятийным мышлением не очень хорошо, но которые умеют ловко говорить и завертывать свои идеи в красивые обертки.

-- Это российская статистика. А как выглядит ситуация в мире?

-- Если брать развитые страны, то приблизительно так же. Могу сослаться на исследования Льва Веккера, который работал и в СССР, и в США, и в Европе, и в России. Его исследования 1998 года показывают, что больше 70% взрослых людей, психологов, с которыми он сотрудничал в ходе исследования мышления детей, и сами мыслят как дети: обобщают от частного к частному, а не по существенному признаку, не видят причинно-следственные связи…

...По жизни сформировать понятийное мышление невозможно, оно приобретается только в ходе изучения наук, поскольку сами науки построены по понятийному принципу: в их основе базовые понятия, над которыми выстраивается пирамида науки. Такая понятийная пирамида. И, если мы выходим из школы без понятийного мышления, то, сталкиваясь с тем или иным фактом, мы не сможем его объективно интерпретировать, а действуем под влиянием эмоций и наших субъективных представлений....

-- Школьные программы последние двадцать лет беспрерывно меняются. Как это влияет на формирование понятийного мышления?

-- Раньше основы понятийного мышления начинали закладываться на природоведении. Теперь у нас вместо природоведения «Окружающий мир». Вы видели, что это такое? Это бессмысленная окрошка. Видеть в этом логику могут только составители, у которых у самих нет понятийного мышления. Якобы это практико-ориентированный, исследовательский предмет. Ничего там этого нет.

Дальше, раньше с 5-го класса начинались ботаника и история как история развития цивилизаций. Теперь у нас в 5 классе природоведение в виде рассказов о природе без всякой логики, а вместо истории цивилизаций - «История в картинках» - та же окрошка без логики, что-то про первобытных людей, что-то про рыцарей.

В шестом-седьмом классах раньше была зоология, опять же со своей логикой. Дальше в восьмом была анатомия, и уже в старшей школе общая биология. То есть, выстраивалась некая пирамида: растительный и животный мир, которые, в конце концов, подчинены общим законам развития. Теперь ничего этого нет. Все идет вперемешку – и ботаника, и животный мир, и человек, и общая биология. Принцип научной подачи информации заменен принципом калейдоскопа, сменяющихся картинок, который разработчики считают системно-деятельностным подходом.

С физикой такая же картина. Тоже рассказы о космосе, о планетах, о законах Ньютона… Вот, сидит у меня мальчик, я его спрашиваю: «Хоть задачки-то решаете на физике?». Он отвечает: «Какие задачки? Мы презентации делаем». Что такое презентация? Это пересказ в картинках. Если нет задач по механике на разложение сил, то о формировании понятийного мышления в физике можно не говорить.

-- Но у нас же декларируется, что мы движемся в сторону европейского и американского образования. Что там-то творится?

-- Там все по-разному. На Западе действительно полная свобода, и школы существуют очень разные. В том числе и такие, куда отбирают не по кошельку, а по уровню развития. И там, безусловно, есть школы отличного уровня, где готовят элиту, обладающую и понятийным и абстрактным мышлением. Но никакого стремления отлично образовывать всех и каждого там нет – зачем это надо?..

...Интересный пример - Финляндия. Всеми признано, что там сейчас лучшая система образования в Европе. Так вот, они как раз взяли наши советские программы и принципы образования. У нас не так давно была конференция по вопросам образования, и там выступила одна наша высокопоставленная дама, автор многих из последних нововведений. Она с гордостью провозгласила, что наконец-то мы уходим от всех этих мифов о хорошем советском образовании. В ответ выступила представитель Финляндии и сказала – извините, но советская система образования в школе была отличная, и мы как раз у вас и заимствовали многое, что позволило нам улучшить нашу систему. Они и учебники наши перевели, и учителей старой школы с большим удовольствием берут, чтобы они делились с их учителями советским методикам преподавания.

-- А у нас, если я вас правильно понимаю, интеллектуальный уровень снижается, и процент людей с понятийным мышлением становится меньше?

-- Да, и это не мои предположения, а данные исследований, которые я веду в школах уже больше двадцати лет, из года в год.

-- Может быть, взамен этого у детей формируются какие-то другие важные качества, помогающие в жизни?

-- К сожалению, нет. Потери в школе видны, а приобретений пока что нет.

... Знаете, у меня есть своя гипотеза, довольно циничная, относительно образовательной политики нашего руководства. Мы сырьевая страна третьего мира. Нам не надо много людей с хорошим образованием и умением думать и делать выводы. Их некуда трудоустроить, они тут никому не нужны.

На образование при этом тратятся огромные деньги, действительно огромные. И что происходит? Наши высокообразованные специалисты уезжают и работают в более развитых странах по всему миру. Целые компании русских программистов работают в США, например. Я знаю одну такую в Бостоне, у них вообще все, кроме уборщицы-негритянки, русские.

Зачем нашему правительству готовить высококвалифицированные кадры для США, Канады, Австралии, Европы? А вы знаете, что в США даже есть математические школы на русском языке с нашими методиками? И те, кто закончили эти школы, отлично устраивают свою жизнь. Но нашей стране эти люди ни к чему.

...Раньше у нас учебники писали математики, физики, биологи, теперь этим занимаются педагоги и психологи. Эти люди не специалисты в предмете, который излагают. На этом образование заканчивается....

Также см.:

• Коренная причина падения качества отечественного математического образования — Костенко И.П.
• В России рушат традиции обучения математике — А. Шевкин